某产品的长度x服从正态分布N(10.88,0.072),规定x在范围(10.74,11.02)(厘米)内为合格品,则产品为合格品的概率为( )(计算时供选用的数据:φ(0)=0.5,φ(1)=0.8413,φ(2)=0.9772,φ(3)=0.9987)
A.0.6826
B.0.3174
C.0.9772
D.0.9544
【答案】
分析:变量服从正态分布N(10.88,0.07
2),即服从均值为10.88,方差为0.07
2的正态分布,适合产品的长度x在(10.74,11.02)范围内取值即在(μ-2σ,μ+2σ)内取值,其概率为:0.9544,从而得出结果.
解答:解:∵产品的长度x服从正态分布N(10.88,0.07
2),
即服从均值为10.88,方差为0.07
2的正态分布,
∵适合产品的长度x在(10.74,11.02)范围内取值即在(μ-2σ,μ+2σ)内取值,
设ξ=
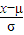
,则ξ服从标准正态分布,
x在(10.74,11.02)范围内取值的概率=ξ在(-2,2)范围内取值的概率,
其概率为:2φ(2)-1=0.9544,
则产品为合格品的概率为0.9544.
故选D.
点评:本题考查正态分布曲线的特点及曲线所表示的意义,考查曲线的变化特点,本题是一个基础题,不需要多少运算

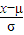 ,则ξ服从标准正态分布,
,则ξ服从标准正态分布,
