
为了治理“沙尘暴”,西部某地区政府经过多年努力,到2009年底,将当地沙漠绿化了40%,从2010年开始,每年将出现这种现象:原有沙漠面积的12%被绿化,即改造为绿洲(被绿化的部分叫绿洲),同时原有绿洲面积的8%又被侵蚀为沙漠,问至少经过几年的绿化,才能使该地区的绿洲面积超过50%?(可参考数据lg2=0.3,最后结果精确到整数).
至少需要4年才能使绿化面积超过50%
设该地区总面积为1,2006年底绿化面积为a1=![]() ,经过n年后绿洲面积为an+1,设2009年底沙漠面积为b1,经过n年后沙漠面积为bn+1,则a1+b1=1,an+bn=1.
,经过n年后绿洲面积为an+1,设2009年底沙漠面积为b1,经过n年后沙漠面积为bn+1,则a1+b1=1,an+bn=1.
依题意an+1由两部分组成:一部分是原有绿洲an减去被侵蚀的部分8%·an的剩余面积92%·an,另一部分是新绿化的12%·bn,所以
an+1=92%·an+12%(1-an)=![]() an+
an+![]() ,即an+1-
,即an+1-![]() =
=![]() (an-
(an-![]() ),
),
∴![]() 是以-
是以-![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
则an+1=![]() -
-![]()
![]() n,
n,
∵an+1>50%,∴![]() -
-![]()
![]() n>
n>![]() ,
,
∴![]() n ﹤
n ﹤![]() ,n>log
,n>log![]()
![]() =
=![]() =3.
=3.
则当n≥4时,不等式![]() n ﹤
n ﹤![]() 恒成立.
恒成立.
所以至少需要4年才能使绿化面积超过50%.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:志鸿系列训练必修一数学北师版 题型:013
为了治理沙尘暴,A市政府大力加强环境保护,其周边草场绿色植被面积每年都比上一年增长10.4%,那么经过x年绿色植被的面积为y,则y=f(x)的图像大致为
A.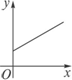
B.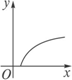
C.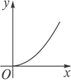
D.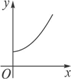
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com