
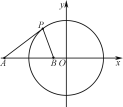
【题目】已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
(1)求与圆C相切,且与直线l垂直的直线方程;
(2)在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.
【答案】(1)y=-2x±3![]() (2)
(2)![]()
【解析】(1)设所求直线方程为y=-2x+b,即2x+y-b=0,
∵直线与圆相切,∴![]() =3,得b=±3
=3,得b=±3![]() ,∴所求直线方程为y=-2x±3
,∴所求直线方程为y=-2x±3![]() .
.
(2)(解法1)假设存在这样的点B(t,0),
当P为圆C与x轴左交点(-3,0)时,![]() =
=![]() ;
;
当P为圆C与x轴右交点(3,0)时,![]() =
=![]() ,
,
依题意,![]() =
=![]() ,解得,t=-5(舍去),或t=-
,解得,t=-5(舍去),或t=-![]() .
.
下面证明点B![]() 对于圆C上任一点P,都有
对于圆C上任一点P,都有![]() 为一常数.
为一常数.
设P(x,y),则y2=9-x2,
∴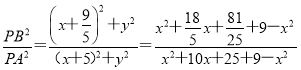 =
= ,从而
,从而![]() =
=![]() 为常数.
为常数.
(解法2)假设存在这样的点B(t,0),使得![]() 为常数λ,则PB2=λ2PA2,∴(x-t)2+y2=λ2[(x+5)2+y2],将y2=9-x2代入得,x2-2xt+t2+9-x2=λ2(x2+10x+25+9-x2),即
为常数λ,则PB2=λ2PA2,∴(x-t)2+y2=λ2[(x+5)2+y2],将y2=9-x2代入得,x2-2xt+t2+9-x2=λ2(x2+10x+25+9-x2),即
2(5λ2+t)x+34λ2-t2-9=0对x∈[-3,3]恒成立,
∴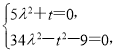 解得
解得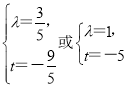 (舍去),
(舍去),
所以存在点B![]() 对于圆C上任一点P,都有
对于圆C上任一点P,都有![]() 为常数
为常数![]()


科目:高中数学 来源: 题型:
【题目】某服装商场为了了解毛衣的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:

(1) 算出线性回归方程![]() ; (a,b精确到十分位)
; (a,b精确到十分位)
(2)气象部门预测下个月的平均气温约为3℃,据此估计,求该商场下个月毛衣的销售量.
(参考公式: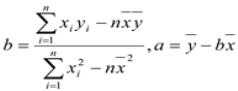 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥![]() 中底面边长为
中底面边长为![]() ,侧棱PA与底面ABCD所成角的正切值为
,侧棱PA与底面ABCD所成角的正切值为![]() .
.
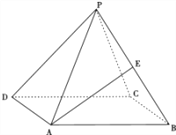
(I)求正四棱锥![]() 的外接球半径;
的外接球半径;
(II)若![]() 是
是![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, ![]() ,AB=2CD=8.
,AB=2CD=8.
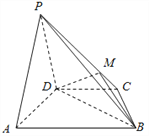
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
查看答案和解析>>
科目:高中数学 来源: 题型:
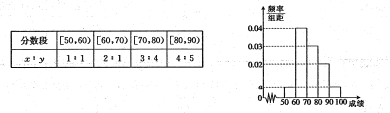
【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,
之比如下表所示,
求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com