
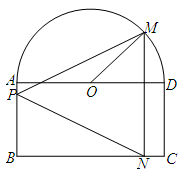
如图所示,一个半圆和长方形组成的铁皮,长方形的边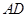 为半圆的直径,
为半圆的直径,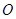 为半圆的圆心,
为半圆的圆心, ,
,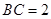 ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形 ,其底边
,其底边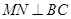 .
.
(1)设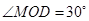 ,求三角形铁皮
,求三角形铁皮 的面积;
的面积;
(2)求剪下的铁皮三角形 的面积的最大值.
的面积的最大值.
(1)三角形铁皮 的面积为
的面积为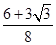 ;(2)剪下的铁皮三角形
;(2)剪下的铁皮三角形 的面积的最大值为
的面积的最大值为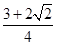 .
.
解析试题分析:(1)利用锐角三角函数求出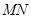 和
和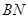 的长度,然后以
的长度,然后以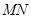 为底边、以
为底边、以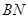 为高,利用三角形面积公式求出三角形
为高,利用三角形面积公式求出三角形 的面积;(2)设
的面积;(2)设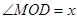 ,以锐角
,以锐角 为自变量将
为自变量将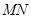 和
和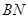 的长度表示出来,并利用面积公式求出三角形
的长度表示出来,并利用面积公式求出三角形 的面积的表达式
的面积的表达式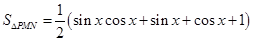 ,利用
,利用 与
与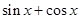 之间的关系
之间的关系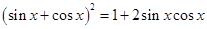 ,令
,令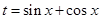 将三角形
将三角形 的面积的表达式表示为以
的面积的表达式表示为以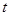 为自变量的二次函数,利用二次函数的单调性求出三角形
为自变量的二次函数,利用二次函数的单调性求出三角形 的面积的最大值,但是要注意自变量
的面积的最大值,但是要注意自变量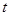 的取值范围作为新函数的定义域.
的取值范围作为新函数的定义域.
试题解析:(1)由题意知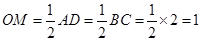 ,
,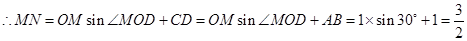 ,
,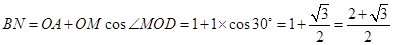 ,
,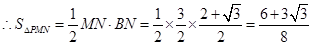 ,即三角形铁皮
,即三角形铁皮 的面积为
的面积为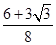 ;
;
(2)设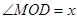 ,则
,则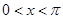 ,
,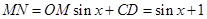 ,
,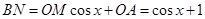 ,
,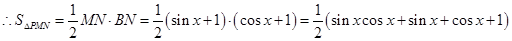 ,
,
令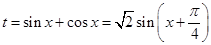 ,由于
,由于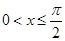 ,所以
,所以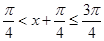 ,
,
则有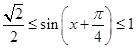 ,所以
,所以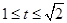 ,
,
且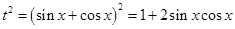 ,所以
,所以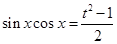 ,
,
故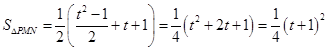 ,
,
而函数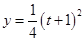 在区间
在区间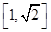 上单调递增,
上单调递增,
故当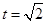 时,
时,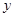 取最大值,即
取最大值,即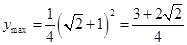 ,
,
即剪下的铁皮三角形 的面积的最大值为
的面积的最大值为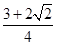 .
.
考点:1.三角形的面积;2.三角函数的最值;3.二次函数的最值


科目:高中数学 来源: 题型:解答题
张林在李明的农场附近建了一个小型工厂,由于工厂生产须占用农场的部分资源,因此李明每年向张林索赔以弥补经济损失并获得一定净收入.工厂在不赔付农场的情况下,工厂的年利润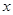 (元)与年产量
(元)与年产量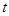 (吨)满足函数关系
(吨)满足函数关系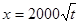 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场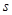 元(以下称
元(以下称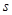 为赔付价格).
为赔付价格).
(Ⅰ)将工厂的年利润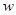 (元)表示为年产量
(元)表示为年产量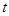 (吨)的函数,并求出工厂获得最大利润的年产量;
(吨)的函数,并求出工厂获得最大利润的年产量;
(Ⅱ)若农场每年受工厂生产影响的经济损失金额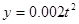 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格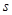 是多少?
是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某公司生产品牌服装的年固定成本是10万元,每生产千件,须另投入2 7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且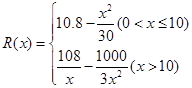
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大?(注:年利润=年销售收入 年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一家公司生产某种产品的年固定成本为10万元,每生产1千件该产品需另投入2.7万元,设该公司一年内生产该产品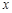 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为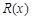 万元,且
万元,且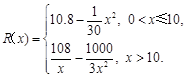
(Ⅰ)写出年利润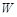 (万元)关于年产量
(万元)关于年产量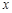 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一产品的产销过程中所获利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com