
| 分组 | 频数 | 频率 |
| [-3,-2) | ① | 0.10 |
| [-2,-1) | 8 | 0.16 |
| (1,2] | ② | 0.50 |
| (2,3] | 10 | ③ |
| (3,4] | ④ | 0.04 |
| 合计 | 50 | 1.00 |
分析 (1)根据频率分布表,利用频率、频数与样本容量的关系计算表中对应的数据即可;
(2)用频率计算不合格的直径长与标准值的差落在(1,3]内的概率值;
(3)利用比例关系计算合格品数即可.
解答 解:(1)根据频率分布表,得
①中数据为50×0.1=5;
②中数据为50×0.5=25;
③中数据为$\frac{10}{50}$=0.2;
④中数据为50×0.04=2;…(2分)
(2)不合格的直径长与标准值的差落在(1,3]内的概率为
0.50+0.20=0.70;----(7分)
(3)设合格品数为x,依题意,得
$\frac{50}{5000}$=$\frac{20}{x+20}$,
解得x=1980,
所以,这批次合格品件数为1980.-----(12分)
点评 本题考查了频率分布表的应用问题,也考查了分析与计算能力,是基础题目.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{7π}{12},0)$是函数y=f(x)的对称中心 | B. | $x=\frac{7π}{12}$是函数y=f(x)的对称轴 | ||
| C. | $(-\frac{π}{12},0)$是函数y=f(x)的对称中心 | D. | $x=-\frac{π}{12}$是函数y=f(x)的对称轴 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2}]$ | B. | (0,+∞) | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.
如图,已知F(1,0)为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,离心率$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
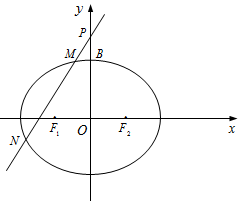 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左,右焦点分别为F1,F2,上顶点为B.Q为抛物线y2=24x的焦点,且$\overrightarrow{{F_1}B}•\overrightarrow{QB}=0$,$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{Q{F_1}}$=0查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com