
【题目】已知![]() 为定义在
为定义在![]() 上的偶函数,
上的偶函数,![]() ,且当
,且当![]() 时,
时,![]() 单调递增,则不等式
单调递增,则不等式![]() 的解集为__________.
的解集为__________.
【答案】![]()
【解析】
根据题意,分析可得f(x+1)﹣f(x+2)>2x+3f(x+1)+(x+1)2>f(x+2)+(x+2)2g(x+1)>g(x+2),由函数奇偶性的定义分析可得g(x)为偶函数,结合函数的单调性分析可得g(x+1)>g(x+2)|x+1|>|x+2|,解可得x的取值范围,即可得答案.
根据题意,g(x)=f(x)+x2,
则f(x+1)﹣f(x+2)>2x+3f(x+1)+(x+1)2>f(x+2)+(x+2)2g(x+1)>g(x+2),
若f(x)为偶函数,则g(﹣x)=f(﹣x)+(﹣x)2=f(x)+x2=g(x),即可得函数g(x)为偶函数,
又由当x∈(﹣∞,0]时,g(x)单调递增,则g(x)在[0,+∞)上递减,
则g(x+1)>g(x+2)|x+1|<|x+2|(x+1)2<(x+2)2,解可得x![]() ,
,
即不等式的解集为(![]() ,+∞);
,+∞);
故答案为:(![]() ,+∞).
,+∞).


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】如果有一天我们分居异面直线的两头,那我一定穿越时空的阻隔,画条公垂线向你冲来,一刻也不愿逗留.如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.
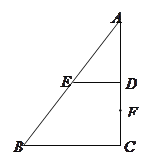

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛掷一蓝、一黄两枚质地均匀的正四面体骰子,分别观察底面上的数字.

(1)用表格表示试验的所有可能结果;
(2)列举下列事件包含的样本点:A=“两个数字相同”,B=“两个数字之和等于5”,C=“蓝色骰子的数字为2”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,等边△ABC中,AC=4,D是边AC上的点(不与A,C重合),过点D作DE∥BC交AB于点E,沿DE将△ADE向上折起,使得平面ADE⊥平面BCDE,如图2所示.
(1)若异面直线BE与AC垂直,确定图1中点D的位置;
(2)证明:无论点D的位置如何,二面角D﹣AE﹣B的余弦值都为定值,并求出这个定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列说法是否正确,若错误,请举出反例
(1)互斥的事件一定是对立事件,对立事件不一定是互斥事件;
(2)互斥的事件不一定是对立事件,对立事件一定是互斥事件;
(3)事件![]() 与事件B中至少有一个发生的概率一定比
与事件B中至少有一个发生的概率一定比![]() 与B中恰有一个发生的概率大;
与B中恰有一个发生的概率大;
(4)事件![]() 与事件B同时发生的概率一定比
与事件B同时发生的概率一定比![]() 与B中恰有一个发生的概率小.
与B中恰有一个发生的概率小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com