
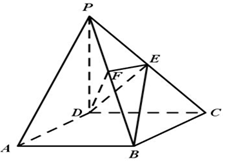
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC中点,作EF⊥PB,交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC中点,作EF⊥PB,交PB于点F.分析 (1)利用线面平行的判定定理证明线面平行.
(2)利用线面垂直的判定定理及面面垂直的判定定理即可证明.
(3)利用线面垂直的判定定理证明.
解答 (本小题满分12分)
证明:(1)连AC与BD相交于O,连接OE,
则OE 为△APC的中位线,OE∥PA,
为△APC的中位线,OE∥PA,
又OE?平面EDB,PA?平面EDB,
由线面平行的判定定理知PA∥平面EDB…(3分)
(2)PD=DC,且PD⊥底面ABCD,
∴△PDC为等腰直角三角形,E是PC中点,DE⊥PC,
又底面ABCD为正方形BC⊥DC,
由BC⊥PD,PD∩DC=D,
∴BC⊥平面PDC,而DE?平面PDC,
∴DE⊥BC,又PC∩BC=C,
∴DE⊥平面PBC,DE?平面EFD
故平面EFD⊥平面PBC…(9分)
(3)由(2)知,DE⊥平面PBC,PB?平面PBC,
∴PB⊥DE,
又PB⊥EF,EF∩DE=E,
∴PB⊥平面EFD.…(12分)
点评 本题主要考查线面平行、面面垂直和线面垂直的判定,考查了空间想象能力和推理论证能力,要求熟练掌握相应的判定定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
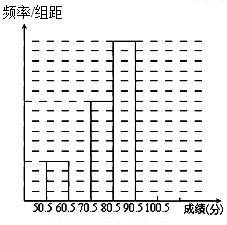 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 6 | 0.08 |
| 60.5~70.5 | 12 | 0.16 |
| 70.5~80.5 | 15 | 0.2 |
| 80.5~90.5 | 24 | 0.32 |
| 90.5~100.5 | 18 | 0.24 |
| 合计 | 75 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{21}{8}$ | B. | $\frac{21}{8}$ | C. | -9 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com