
【题目】某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试![]() 假设某学生每次通过测试的概率都是
假设某学生每次通过测试的概率都是![]() ,每次测试时间间隔恰当,每次测试通过与否互相独立.
,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1)求该学生考上大学的概率.
(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为X,求X的概率分布及X的数学期望.
科目:高中数学 来源: 题型:
【题目】随着现代社会的发展,我国对于环境保护越来越重视,企业的环保意识也越来越强.现某大型企业为此建立了5套环境监测系统,并制定如下方案:每年企业的环境监测费用预算定为1200万元,日常全天候开启3套环境监测系统,若至少有2套系统监测出排放超标,则立即检查污染源处理系统;若有且只有1套系统监测出排放超标,则立即同时启动另外2套系统进行1小时的监测,且后启动的这2套监测系统中只要有1套系统监测出排放超标,也立即检查污染源处理系统.设每个时间段(以1小时为计量单位)被每套系统监测出排放超标的概率均为![]() ,且各个时间段每套系统监测出排放超标情况相互独立.
,且各个时间段每套系统监测出排放超标情况相互独立.
(1)当![]() 时,求某个时间段需要检查污染源处理系统的概率;
时,求某个时间段需要检查污染源处理系统的概率;
(2)若每套环境监测系统运行成本为300元/小时(不启动则不产生运行费用),除运行费用外,所有的环境监测系统每年的维修和保养费用需要100万元.现以此方案实施,问该企业的环境监测费用是否会超过预算(全年按9000小时计算)?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三陵锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点.
的中点.
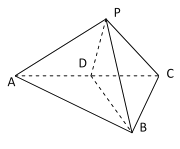
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角为锐角,且棱锥
的平面角为锐角,且棱锥![]() 的体积为
的体积为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
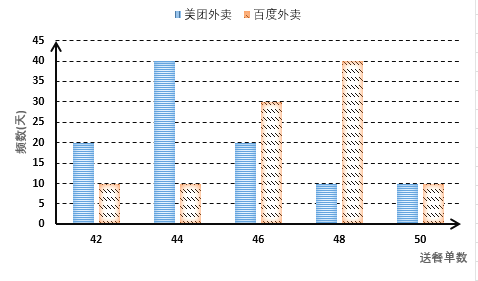
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com