Question

【题目】在中，角所对的边分别为.

（1）若为边的中点，求证: ;

（2）若，求面积的最大值.

Answer 1

【答案】（1）详见解析；（2）1.

【解析】

（1）证法一：根据为边的中点，可以得到向量等式，平方，再结合余弦定理，可以证明出等式；

证法二：分别在和中，利用余弦定理求出和的表达式，利用，可以证明出等式；

（2）解法一：解法一：记面积为．由题意并结合（1）

所证结论得：，利用已知

，再结合基本不等式，最后求可求出面积的最大值；

解法二：利用余弦定理把表示出来，结合重要不等式，再利用三角形面积公式可得

，令设，利用辅助角公式，可以求出的最大值，即可求出面积的最大值.

（1）证法一：由题意得

①

由余弦定理得 ②

将②代入①式并化简得，

故；

证法二：在中，由余弦定理得，

在中，由余弦定理得，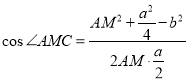

∵，∴，

则，故；

（2）解法一：记面积为．由题意并结合（1）

所证结论得：，

又已知，

则，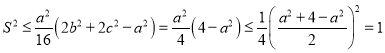

即，当时，等号成立，故，

即面积的最大值为1．

解法二：

设

则

由，

故.