
【题目】已知⊙H被直线x-y-1=0,x+y-3=0分成面积相等的四个部分,且截x轴所得线段的长为2。
(I)求⊙H的方程;
(Ⅱ)若存在过点P(0,b)的直线与⊙H相交于M,N两点,且点M恰好是线段PN的中点,求实数b的取值范围
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(I)设![]() 的方程为
的方程为![]() ,由题意可知圆心
,由题意可知圆心![]() 一定是两直线
一定是两直线![]() 的交点,可得交点为
的交点,可得交点为![]() ,所以
,所以![]() . 又
. 又![]() 截x轴所得线段的长为2,所以
截x轴所得线段的长为2,所以![]() .,即可得到⊙H的方程;
.,即可得到⊙H的方程;
(II)法一:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,
,
过点N作![]() 的直径
的直径![]() ,连结
,连结![]() .
.
由题可得“点![]() 是线段
是线段![]() 的中点”等价于“圆上存在一点
的中点”等价于“圆上存在一点![]() 使得
使得![]() 的长等于
的长等于![]() 的直径”.
的直径”.
由此得到实数b的取值范围
法二:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,连结
,连结![]() ,
,
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,并设
,并设![]() .
.
由题意得![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,由此得到实数b的取值范围
,由此得到实数b的取值范围
试题解析:(I)设![]() 的方程为
的方程为![]() ,
,
因为![]() 被直线
被直线![]() 分成面积相等的四部分,
分成面积相等的四部分,
所以圆心![]() 一定是两直线
一定是两直线![]() 的交点,
的交点,
易得交点为![]() ,所以
,所以![]() .
.
又![]() 截x轴所得线段的长为2,所以
截x轴所得线段的长为2,所以![]() .
.
所以![]() 的方程为
的方程为![]() .
.
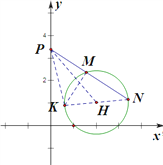
(II)法一:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,
,
过点N作![]() 的直径
的直径![]() ,连结
,连结![]() .
.
当![]() 与
与![]() 不重合时,
不重合时, ![]() ,
,
又点![]() 是线段
是线段![]() 的中点
的中点![]() ;
;
当![]() 与
与![]() 重合时,上述结论仍成立.
重合时,上述结论仍成立.
因此,“点![]() 是线段
是线段![]() 的中点”等价于“圆上存在一点
的中点”等价于“圆上存在一点![]() 使得
使得![]() 的长等于
的长等于![]() 的直径”.
的直径”.
由图可知![]() ,即
,即![]() ,即
,即![]() .
.
显然![]() ,所以只需
,所以只需![]() ,即
,即![]() ,解得
,解得![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.

法二:如图, ![]() 的圆心
的圆心![]() ,半径
,半径![]() ,连结
,连结![]() ,
,
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,并设
,并设![]() .
.
由题意得![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
将![]() 代入整理可得
代入整理可得![]() ,
,
因为![]() ,所以
,所以![]() ,,解得
,,解得![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
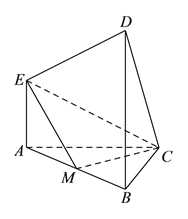
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .若存在,指出点
.若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 过抛物线焦点,且与抛物线交于
过抛物线焦点,且与抛物线交于![]() ,
, ![]() 两点,以线段
两点,以线段![]() 为直径的圆与抛物线准线的位置关系是( )
为直径的圆与抛物线准线的位置关系是( )
A. 相离 B. 相交 C. 相切 D. 不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=a(x-5)2+6lnx,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线与y轴相交于点(0,6).
(1)确定a的值;
(2)求函数f(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李,小王设计的底座形状分别为![]() ,
, ![]() ,经测量
,经测量![]() 米,
米, ![]() 米,
米, ![]() 米,
米, ![]()
(I)求![]() 的长度;
的长度;
(Ⅱ)若环境标志的底座每平方米造价为![]() 元,不考虑其他因素,小李,小王谁的设计建造费用最低(请说明理由),最低造价为多少?(
元,不考虑其他因素,小李,小王谁的设计建造费用最低(请说明理由),最低造价为多少?(![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() 是棱PD的中点,且
是棱PD的中点,且![]() ,
, ![]() .
.
(I)求证: ![]() ; (Ⅱ)求二面角
; (Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 是
是![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 成角的正弦值为
成角的正弦值为![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月3日,抗战胜利71周年纪念活动在北京隆重举行,受到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、拥待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这个环节(可参加多个,也可都不参加)的情况及其概率如下表所示:

(Ⅰ)若m=2n,则从这60名抗战老兵中按照参加纪念活动的环节数分层抽取6人进行座谈,求从参加纪念活动环节数为1的抗战老兵中抽取的人数;
(Ⅱ)某医疗部门决定从(Ⅰ)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
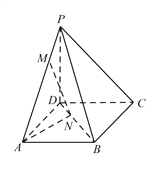
【题目】如图,四棱锥 ![]() 底面为正方形,已知
底面为正方形,已知 ![]() ,
,![]() ,点
,点 ![]() 为线段
为线段 ![]() 上任意一点(不含端点),点
上任意一点(不含端点),点 ![]() 在线段
在线段 ![]() 上,且
上,且 ![]() .
.
(1)求证:![]() ;
;
(2)若 ![]() 为线段
为线段 ![]() 中点,求直线
中点,求直线 ![]() 与平面
与平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com