
某射手每次射击击中目标的概率均为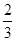 ,且每次射击的结果互不影响
,且每次射击的结果互不影响
(I)假设这名射手射击3次,求至少2次击中目标的概率
(II)假设这名射手射击3次,每次击中目标10分,未击中目标得0分,在3次射击中,若有两次连续击中目标,而另外一次未击中目标,则额外加5分;若3次全部击中,则额外加10分。用随机变量§表示射手射击3次后的总得分,求§的分布列和数学期望。
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: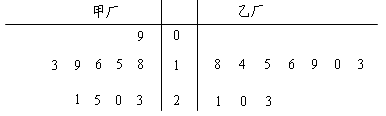
规定:当产品中的此种元素含量不小于18毫克时,该产品为优等品.
(1)试用上述样本数据估计甲、乙两厂生产的优等品率;
(2)从乙厂抽出的上述10件样品中,随机抽取3件,求抽到的3件样品中优等品数 的分布列及其数学期望
的分布列及其数学期望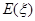 ;
;
(3)从甲厂的10件样品中有放回的随机抽取3件,也从乙厂的10件样品中有放回的随机抽取3件,求抽到的优等品数甲厂恰比乙厂多2件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为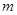 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为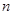 ,求
,求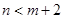 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 105 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分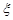 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间共有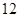 名工人,随机抽取
名工人,随机抽取 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 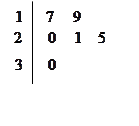
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间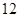 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间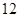 名工人中,任取
名工人中,任取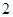 人,求恰有
人,求恰有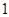 名优秀工人的概率.
名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
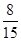 .
.| P(K2>k) | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.841 | 5.024 | 6.635 | 7.879 |
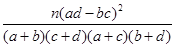 ,其中n="a+b+c+d)"
,其中n="a+b+c+d)" 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示.经销商为下一个销售季度购进了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.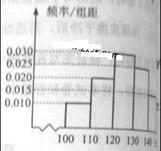
(Ⅰ)将T表示为x的函数
(Ⅱ)根据直方图估计利润T不少于57000元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x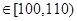 ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110 ,求T的数学期望.
,求T的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率为 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是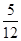 ,得到黄球或绿球的概率是
,得到黄球或绿球的概率是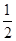 ,试求得到黑球、黄球、绿球的概率各是多少?
,试求得到黑球、黄球、绿球的概率各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com