
【题目】设f(x)、g(x)、h(x)是定义域为R的三个函数,对于命题:①f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均为增函数,则f(x)、g(x)、h(x)中至少有一个增函数;②若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是以T为周期的函数,则f(x)、g(x)、h(x)均是以T为周期的函数,下列判断正确的是( )
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题,②为假命题
D.①为假命题,②为真命题
【答案】D
【解析】解:①不成立.可举反例:f(x)=![]() .g(x)=
.g(x)=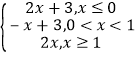 ,h(x)=
,h(x)=![]() .
.
②∵f(x)+g(x)=f(x+T)+g(x+T),f(x)+h(x)=f(x+T)+h(x+T),h(x)+g(x)=h(x+T)+g(x+T),
前两式作差可得:g(x)﹣h(x)=g(x+T)﹣h(x+T),结合第三式可得:g(x)=g(x+T),h(x)=h(x+T),同理可得:f(x)=f(x+T),因此②正确.
故选:D.
①不成立.可举反例:f(x)= ![]() .g(x)=
.g(x)= 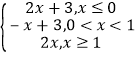 ,h(x)=
,h(x)= ![]() .
.
②由题意可得:f(x)+g(x)=f(x+T)+g(x+T),f(x)+h(x)=f(x+T)+h(x+T),h(x)+g(x)=h(x+T)+g(x+T),
可得:g(x)=g(x+T),h(x)=h(x+T),f(x)=f(x+T),即可判断出真假.;本题考查了函数的单调性与周期性、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以O为极点,x轴正半轴为极轴建立直角坐标系,圆C的极坐标方程为
中,以O为极点,x轴正半轴为极轴建立直角坐标系,圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线![]() 和圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
和圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(1)求圆心的极坐标;(2)求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如下表:

(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区![]() 年该农产品的产量;
年该农产品的产量;
②当![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体EF-ABCD中,四边形CDEF是正方形,四边形ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB是腰长为2![]() 的等腰直角三角形,平面CDEF⊥平面ABCD.
的等腰直角三角形,平面CDEF⊥平面ABCD.
(1)求证:BC⊥AF;
(2)求几何体EF-ABCD的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=a(x﹣lnx)+ ![]() ,a∈R.
,a∈R.
(1)讨论f(x)的单调性;
(2)当a=1时,证明f(x)>f′(x)+ ![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设an=1+![]() +=
+=![]() +…+
+…+![]() (n∈N*),是否存在一次函数g(x),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切正整数都成立?并试用数学归纳法证明你的结论.
(n∈N*),是否存在一次函数g(x),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切正整数都成立?并试用数学归纳法证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2﹣a﹣lnx,其中a∈R.
(1)讨论f(x)的单调性;
(2)确定a的所有可能取值,使得f(x)> ![]() ﹣e1﹣x在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
﹣e1﹣x在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com