
某超市中秋前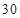 天月饼销售总量
天月饼销售总量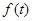 与时间
与时间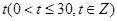 的关系大致满足
的关系大致满足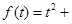
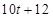 ,则该超市前
,则该超市前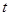 天平均售出(如前
天平均售出(如前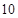 天的平均售出为
天的平均售出为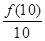 )的月饼最少为____________.
)的月饼最少为____________.
科目:高中数学 来源: 题型:填空题
下列几个命题:
①方程 有一个正实根,一个负实根,则
有一个正实根,一个负实根,则 ;
;
②函数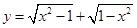 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③设函数 定义域为R,则函数
定义域为R,则函数 与
与 的图象关于
的图象关于 轴对称;
轴对称;
④一条曲线 和直线
和直线 的公共点个数是
的公共点个数是 ,则
,则 的值不可能是
的值不可能是 .其中正确的有______________.
.其中正确的有______________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列五个命题中,其中所有正确命题的序号是_______.
①函数 的最小值是3
的最小值是3
②函数 若
若 且
且 ,则动点
,则动点 到直线
到直线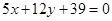 的
的
最小距离是 .
.
③命题“函数 当
当
 ”是真命题.
”是真命题.
④函数 的最小正周期是1的充要条件是
的最小正周期是1的充要条件是 .
.
⑤已知等差数列 的前
的前 项和为
项和为 ,
, 为不共线的向量,又
为不共线的向量,又
若 ,则
,则 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知函数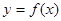 ,
, ,
,
(1) 与
与 的图象关于直线
的图象关于直线 对称;
对称;
(2)有下列4个命题:
①若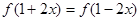 ,则
,则 的图象关于直线
的图象关于直线 对称;
对称;
② 则5是
则5是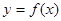 的周期;
的周期;
③若 为偶函数,且
为偶函数,且 ,则
,则 的图象关于直线
的图象关于直线 对称;
对称;
④若 为奇函数,且
为奇函数,且 ,则
,则 的图象关于直线
的图象关于直线 对称.
对称.
其中正确的命题为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com