
分析 (Ⅰ)求出函数的导数,根据f′(1)=$\frac{1}{2}$a,求出a的值,根据g(1)=0,求出b的值,从而求出g(x)的解析式即可;
(Ⅱ)求出φ(x)的导数,问题转化为x2-(2m-2)x+1≥0在[1,+∞)上恒成立,求出m的范围即可;
(Ⅲ)根据$lnx>\frac{2(x-1)}{x+1}$得到:$\frac{1}{lnx}<\frac{1}{2}•\frac{x+1}{x-1}$,对x取值,累加即可.
解答 解:(Ⅰ)由于f(x)与g(x)在x=1处相切
且$f'(x)=\frac{1}{x}$∴$f'(1)=1=\frac{1}{2}a$得:a=2------------------(2分)
又∵$g(1)=0=\frac{1}{2}a+b$∴b=-1∴g(x)=x-1------------------(3分)
(Ⅱ)$φ(x)=\frac{m(x-1)}{x+1}-f(x)$=$\frac{m(x-1)}{x+1}-lnx$在[1,+∞)上是减函数,
∴$ϕ'(x)=\frac{{-{x^2}+(2m-2)x-1}}{{x{{(x+1)}^2}}}≤0$在[1,+∞)上恒成立.------------------(5分)
即x2-(2m-2)x+1≥0在[1,+∞)上恒成立,由$2m-2≤x+\frac{1}{x}$,x∈[1,+∞)
又∵$x+\frac{1}{x}∈[2,+∞)$∴2m-2≤2得m≤2------------------(7分)
(Ⅲ)由(Ⅱ)可得:当m=2时:
ϕ(x)=$\frac{2(x-1)}{x+1}-lnx$在[1,+∞)上是减函数,
∴当x>1时:ϕ(x)<ϕ(1)=0即$\frac{2(x-1)}{x+1}-lnx$<0
所以$lnx>\frac{2(x-1)}{x+1}$从而得到:$\frac{1}{lnx}<\frac{1}{2}•\frac{x+1}{x-1}$------------------(10分)
当x=2时:$\frac{1}{ln2}<\frac{1}{2}•\frac{3}{1}$
当x=3时:$\frac{1}{ln3}<\frac{1}{2}•\frac{4}{2}$
当x=4时:$\frac{1}{ln4}<\frac{1}{2}•\frac{5}{3}$??
当x=n+1时:$\frac{1}{ln(n+1)}<\frac{1}{2}•\frac{n+2}{n}$,n∈N+,n≥2
上述不等式相加得:
$\frac{1}{ln2}+\frac{1}{ln3}+\frac{1}{ln4}+…+\frac{1}{ln(n+1)}$$<\frac{1}{2}(\frac{3}{1}+\frac{4}{2}+\frac{5}{3}+…+\frac{n+2}{n})$
=$\frac{1}{2}(n+\frac{2}{1}+\frac{2}{2}+\frac{2}{3}+…+\frac{2}{n})$=$\frac{n}{2}+1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$
即$\frac{1}{ln2}+\frac{1}{ln3}+\frac{1}{ln4}+…+\frac{1}{ln(n+1)}$$<\frac{n}{2}+1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}$.(n∈N+,n≥2)
------------------(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
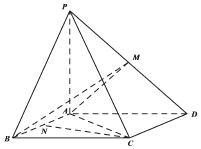 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
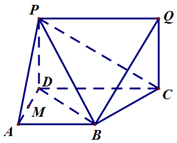 如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,PD⊥面ABCD,QC⊥面ABCD,且AB=AD=PD=QC=$\frac{1}{2}$CD,
如图,在直角梯形ABCD中,AB⊥AD,AB∥CD,PD⊥面ABCD,QC⊥面ABCD,且AB=AD=PD=QC=$\frac{1}{2}$CD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com