
【题目】已知圆O1的方程为x2+(y+1)2=4,圆O2的圆心为O2(2,1).
(1)若圆O1与圆O2外切,求圆O2的方程;
(2)若圆O1与圆O2交于A , B两点,且|AB|=2 ![]() ,求圆O2的方程.
,求圆O2的方程.
【答案】
(1)解:设圆O1、圆O2的半径分别为r1,r2,
∵两圆相切,
∴|O1O2|=r1+r2,∴r2=|O1O2|-r1= ![]() ,
,
∴圆O2的方程是(x-2)2+(y-1)2=4( ![]() -1)2.
-1)2.
(2)解:由题意,设圆O2的方程为(x-2)2+(y-1)2= ![]() ,
,
圆O1,O2的方程相减,即得两圆公共弦AB所在直线的方程,
为4x+4y+ ![]() -8=0.
-8=0.
∴圆心O1(0,-1)到直线AB的距离为 ![]() ,
,
解得 ![]() 或20.
或20.
∴圆O2的方程为(x-2)2+(y-1)2=4或(x-2)2+(y-1)2=20.
【解析】(1)根据两圆外切可知两圆的圆心距等于两圆的半径和,从而可求得圆O2的半径,即可求得圆O2的方程;(2)先设出圆O2的标准方程,从而表示出两圆公共弦所在直线方程,再解公共弦的一般与圆心到弦的距离及圆的半径所组成的三角形即可求得圆O2的半径,从而求得圆O2的方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否做到“光盘”行动,得到如下列联表及附表: 经计算: ![]()
做不到“光盘”行动 | 做到“光盘”行动 | |
男 | 45 | 10 |
女 | 30 | 15 |
P(X2≥x0) | 0.10 | 0.05 | 0.025 |
x0 | 2.706 | 3.841 | 5.024 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市民能否做到‘光盘’行动与性别无关”
C.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别有关”
D.有90%以上的把握认为“该市民能否做到‘光盘’行动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的n位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如右图所示. 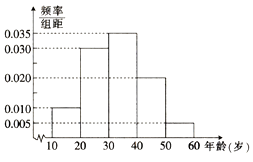
(1)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(2)若按分层抽样的方法从年龄在[20,30)以内及[40,50)以内的市民中随机抽取10人,再从这10人中随机抽取3人进行调研,记随机抽的3人中,年龄在[40,50)以内的人数为X,求X的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知一艘海监船O上配有雷达,其监测范围是半径为25 km的圆形区域,一艘外籍轮船从位于海监船正东40 km的A处出发,径直驶向位于海监船正北30 km的B处岛屿,速度为28 km/h.
问:这艘外籍轮船能否被海监船监测到?若能,持续时间多长?(要求用坐标法)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,三个内角A,B,C依次成等差数列,若sin2B=sinAsinC,则△ABC形状是( )
A.锐角三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且 ![]() ,
, ![]() .
. 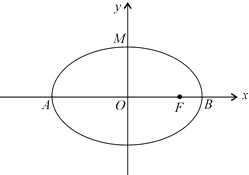
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为M,直线l交椭圆于P,Q两点,问:是否存在直线l,使点F恰为△PQM的垂心?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为得到函数y=sin(2x﹣ ![]() )的图象,只需将函数y=sin2x的图象( )
)的图象,只需将函数y=sin2x的图象( )
A.向左平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向右平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com