
【题目】抛物线![]() 的焦点为
的焦点为![]() ,已知点
,已知点![]() 为抛物线
为抛物线![]() 上的两个动点,且满足
上的两个动点,且满足![]() .过弦
.过弦![]() 的中点
的中点![]() 作抛物线
作抛物线![]() 准线的垂线
准线的垂线![]() ,垂足为
,垂足为![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
设|AF|=a,|BF|=b,连接AF、BF.由抛物线定义得2|MN|=a+b,由余弦定理可得|AB|2=(a+b)2﹣ab,进而根据基本不等式,求得|AB|的取值范围,从而得到本题答案.
设|AF|=a,|BF|=b,连接AF、BF
由抛物线定义,得|AF|=|AQ|,|BF|=|BP|
在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b.
由余弦定理得,
|AB|2=a2+b2﹣2abcos120°=a2+b2+ab
配方得,|AB|2=(a+b)2﹣ab,
又∵ab≤![]()
∴(a+b)2﹣ab≥(a+b)2![]() (a+b)2
(a+b)2![]() (a+b)2
(a+b)2
得到|AB|![]() (a+b).
(a+b).
所以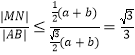 ,即
,即![]() 的最大值为
的最大值为![]() .
.
故选:A.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,两条准线之间的距离为
,两条准线之间的距离为![]() .
.
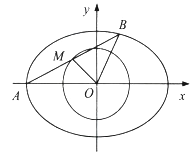
(1)求椭圆的标准方程;
(2)已知椭圆的左顶点为![]() ,点
,点![]() 在圆
在圆![]() 上,直线
上,直线![]() 与椭圆相交于另一点
与椭圆相交于另一点![]() ,且
,且![]() 的面积是
的面积是![]() 的面积的
的面积的![]() 倍,求直线
倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(1,+∞),使得5+|x0|=6.q:x∈(0,+∞),![]() +81x≥a.
+81x≥a.
(1)若a=9,判断命题¬p,p∨q,(¬p)∧(¬q)的真假,并说明理由;
(2)设命题r:x0∈R,x02+2x0+a-9≤0判断r成立是q成立的什么条件,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,是“算经十书”中最重要的一种。在其第七章中有如下问题:“今有蒲生一日,长三尺,莞生一日,长一尺,蒲生日自半,莞生日自倍,问几何日而长等?”意思是植物蒲发芽的第一天长高三尺,植物莞发芽的第一天长高一尺。蒲从第二天开始每天生长速度是前一天的一半,莞从第二天开始每天生长速度为前一天的两倍。问这两种植物在何时高度相同?
在此问题中,蒲和莞高度相同的时刻在( )
A. 第二天 B. 第三天 C. 第四天 D. 第五天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )
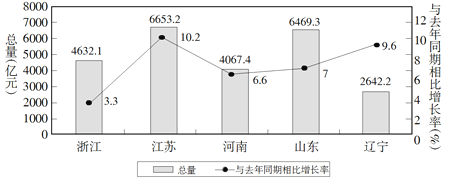
A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com