
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为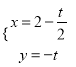 ,(
,( ![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点,过点
上一动点,过点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围是( )
的取值范围是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
直角坐标系![]() 中,直线
中,直线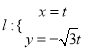 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)分别求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 交曲线
交曲线![]() 于
于![]() 两点,直线
两点,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
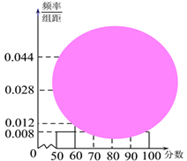
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图:
![]() 求分数在
求分数在![]() 的频率及全班人数;
的频率及全班人数;
![]() 求分数在
求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
![]() 若要从分数在
若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面四边形![]() 中,
中, ![]() ,
, ![]() 为等边三角形,现将
为等边三角形,现将![]() 沿
沿![]() 翻折得到四面体
翻折得到四面体![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.


(Ⅰ)求证:四边形![]() 为矩形;
为矩形;
(Ⅱ)当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|mx|﹣|x﹣n|(0<n<1+m),若关于x的不等式f(x)<0的解集中的整数恰有3个,则实数m的取值范围为( )
A.3<m<6
B.1<m<3
C.0<m<1
D.﹣1<m<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com