
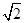 ,求证:a⊥b;
,求证:a⊥b; 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
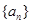 是公比为
是公比为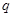 的无穷等比数列,下列
的无穷等比数列,下列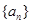 的四组量中,一定能成为该数列“基本量”的是第 组;
的四组量中,一定能成为该数列“基本量”的是第 组;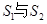 ;②
;②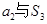 ;③
;③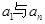 ;④
;④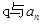 .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
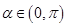 ,且
,且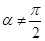 ,当
,当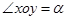 时定义平面坐标系
时定义平面坐标系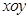 为
为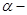 仿射坐标系,在
仿射坐标系,在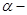 仿射坐标系中,任意一点
仿射坐标系中,任意一点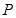 的斜坐标这样定义:
的斜坐标这样定义: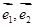 分别为与
分别为与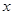 轴、
轴、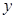 轴正向相同单位向量,若
轴正向相同单位向量,若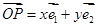 ,则记为
,则记为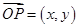 ,那么在以下的结论中,正确的有 .
,那么在以下的结论中,正确的有 .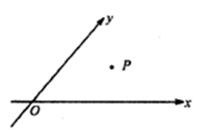
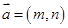 ,
,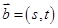 ,若
,若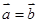 ,则
,则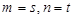 ;
;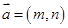 ,则
,则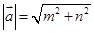 ;
;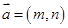 ,
,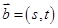 ,若
,若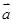
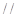
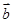 ,则
,则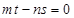 ;
;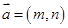 ,
,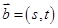 ,若
,若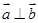 ,
,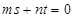 ;
;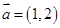 ,
,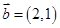 ,若
,若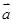 与
与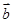 的夹角为
的夹角为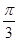 ,则
,则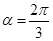 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
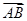 ="(cos" 18°,cos 72°),
="(cos" 18°,cos 72°), 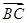 ="(2cos" 63°,2cos 27°),则△ABC面积为( )
="(2cos" 63°,2cos 27°),则△ABC面积为( )A.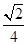 | B. | C.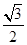 | D.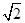 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com