
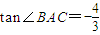 ,且
,且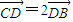 .现建立以A点为坐标原点,以∠BAC的平分线所在直线为x轴的平面直角坐标系,如图所示.
.现建立以A点为坐标原点,以∠BAC的平分线所在直线为x轴的平面直角坐标系,如图所示.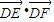 的值.
的值.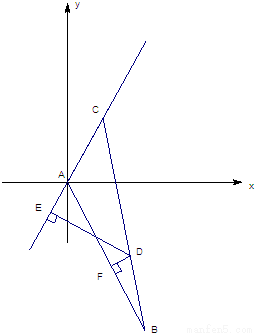
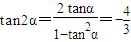 ,从而可直线AC与AB的斜率,进而可求直线方程
,从而可直线AC与AB的斜率,进而可求直线方程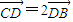 可得得D代入双曲线方程可得点D,结合△ABC的面积为9可求λ即可
可得得D代入双曲线方程可得点D,结合△ABC的面积为9可求λ即可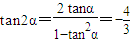
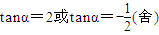
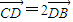
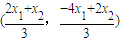
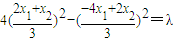 即
即 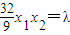
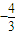 ,得 sin2α=
,得 sin2α=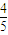 又∵|AB|=
又∵|AB|=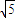 |x1|,|AC|=
|x1|,|AC|=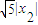
 |AB|•|AC|sinA=
|AB|•|AC|sinA= ×5x1x2•sin2α=9,
×5x1x2•sin2α=9,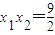 ,代入等式(*),得λ=16.
,代入等式(*),得λ=16.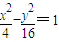
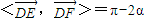 ,所以 cos?
,所以 cos?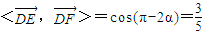 .
.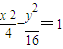 ,
,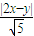 ,DF=
,DF=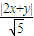
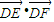 =|DE|•|DF|
=|DE|•|DF|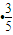 =
=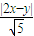 •
•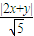
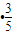 =
=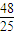


科目:高中数学 来源: 题型:
| 4 |
| 3 |
| CD |
| DB |
| DE |
| DF |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-
(2008•宣武区一模)在面积为9的△ABC中,tan∠BAC=-| 4 |
| 3 |
| CD |
| DB |
| DE |
| DF |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
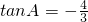 ,且
,且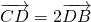 .
.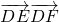 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2010年江西省南昌市新建二中高考数学二模试卷(理科)(解析版) 题型:解答题
 ,且
,且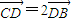 .
.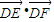 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com