②③④
分析:根据等差数列{a
n}公差为0的情况,得到反例说明①的充分性不成立而错误;根据等比数列的通项与性质,结合已知S
n求的a
n方法,通过正反论证可得②正确;根据四种命题的定义及其相互关系,得到③正确;根据函数奇偶性的定义和二次函数单调性的结论,得到④正确;根据向量的定义和平移的规律,得到⑤错误.由此不难得到正确选项.
解答:对于①,若数列{a
n}是等差数列,若它的公差d=0
则它的通项是a
n=a
1(常数),此时a
n=pn+q(p≠0)不能成立,
说明充分性不成立,不是充要条件,故①错误;
对于②,数列{a
n}的前n项和S
n=ab
n+c
可得当n≥2时,a
n=S
n-S
n-1=ab
n-1(b-1)
当n=1时,a
1=S
1=ab+c
接下来讨论充分性与必要性
若a+c=0,则ab+c=a(b-1)=ab
1-1(b-1),
可得数列的通项为a
n=a(b-1)b
n-1,
∵a≠0,b≠0,b≠1
∴数列{a
n}构成以a(b-1)为首项,公比为b的等比数列.故充分性成立;
反之,若此数列是等比数列,得
∵当n≥2时,a
n=ab
n-1(b-1),公比为b
∴a
2=ab
1(b-1)=ba
1=b(ab+c)
∴-ab=bc?b(a+c)=0
∵b≠0,
∴a+c=0,故必要性成立,说明②正确;
对于③,设命题p:“若A,则B”
则命题p的逆命题q:“若B,则A”,且命题p的否命题r:“若非A,则非B”,
可见q是r的逆否命题,故③正确;
对于④,
∵函数f(x)=ax
2+bx+3a+b是偶函数,其定义域为[a-1,2a],
∴f(-x)=ax
2-bx+3a+b=f(x)且a-1+2a=0
∴b=0且a=

,得函数表达式为f(x)=

x
2+1
在区间(-∞,0)上是减函数,所以f(x)在

上是减函数
故④正确;
对于⑤,因为向量平移后,终点和起点都发生了同样的平移,
故向量的大小与方向均没有变化,故向量
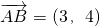
按向量
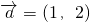
平移后坐标仍为(3,4),故⑤错误.
故答案为②③④
点评:本题借助于充要条件的判断和命题的真假判断与应用,考查了函数奇偶性与单调性、等差数列和等比数列的通项与性质和向量平移等知识点,属于中档题.

 上是减函数;
上是减函数; 平移后为(2,2)
平移后为(2,2) ,得函数表达式为f(x)=
,得函数表达式为f(x)= x2+1
x2+1 上是减函数
上是减函数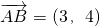 按向量
按向量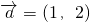 平移后坐标仍为(3,4),故⑤错误.
平移后坐标仍为(3,4),故⑤错误.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案 的解集是(5,4);
的解集是(5,4);