
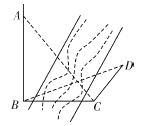
【题目】如图,为测得河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,测得点
的正东方向上,测得点![]() 的仰角为60°,再由点
的仰角为60°,再由点![]() 沿北偏东15°方向走
沿北偏东15°方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是(单位:
的高是(单位:![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在直棱柱ABCD﹣A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3. 
(1)证明:AC⊥B1D;
(2)求直线B1C1与平面ACD1所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n是正整数,r为正有理数.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(参考数据: ![]() .
.
(2)证明: ![]() ;
;
(3)设x∈R,记[x]为不小于x的最小整数,例如 ![]() .令
.令 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比为q,记bn=am(n﹣1)+1+am(n﹣1)+2+…+am(n﹣1)+m , cn=am(n﹣1)+1am(n﹣1)+2…am(n﹣1)+m , (m,n∈N*),则以下结论一定正确的是( )
A.数列{bn}为等差数列,公差为qm
B.数列{bn}为等比数列,公比为q2m
C.数列{cn}为等比数列,公比为 ![]()
D.数列{cn}为等比数列,公比为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年北京市进行人口抽样调查,随机抽取了某区居民
年北京市进行人口抽样调查,随机抽取了某区居民![]() 人,记录他们的年龄,将数据分成
人,记录他们的年龄,将数据分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,…
,…![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(Ⅰ)从该区中随机抽取一人,估计其年龄不小于![]() 的概率;
的概率;
(Ⅱ)估计该区居民年龄的中位数(精确到![]() );
);
(Ⅲ)假设同组中的每个数据用该组区间的中点值代替,估计该区居民的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5. 
(1)求证:AA1⊥平面ABC;
(2)求证二面角A1﹣BC1﹣B1的余弦值;
(3)证明:在线段BC1上存在点D,使得AD⊥A1B,并求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com