
【题目】已知某地区中小学生人数和近视情况如图1和图2所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生作为样本进行调查.

(1)求样本容量和抽取的高中生近视人数分别是多少?
(2)在抽取的![]() 名高中生中,平均每天学习时间超过9小时的人数为
名高中生中,平均每天学习时间超过9小时的人数为![]() ,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
平均学习时间不超过9小时 | 平均学习时间超过9小时 | 总计 | |
不近视 | |||
近视 | |||
总计 |
(3)根据(2)中的列联表,判断是否有![]() 的把握认为高中生平均每天学习时间与近视有关?
的把握认为高中生平均每天学习时间与近视有关?
附:![]() ,其中
,其中![]() .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】下列命题说法中正确的是
A. 对于实数![]() ,“
,“![]() ”是
”是![]() 或
或![]() 的充分不必要条件
的充分不必要条件
B. 已知![]() 都是整数,则命题“若
都是整数,则命题“若![]() ,则
,则![]() 不都是奇数”是假命题
不都是奇数”是假命题
C. “若![]() ,则关于
,则关于![]() 的方程
的方程![]() 有实根”的逆否命题为假命题
有实根”的逆否命题为假命题
D. 命题“全等三角形的面积相等”的否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下面四个命题:
①“若![]() ,则
,则![]() 或
或![]() ”的逆否命题为“若
”的逆否命题为“若![]() 且
且![]() ,则
,则![]() ”
”
②“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
③命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
④若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题,其中真命题个数为( )
均为假命题,其中真命题个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】玉山一中篮球体育测试要求学生完成“立定投篮”和“三步上篮”两项测试,“立定投篮”和“三步上篮”各有2次投篮机会,先进行“立定投篮”测试,如果合格才能参加“三步上篮”测试.为了节约时间,每项测试只需且必须投中一次即为合格.小华同学“立定投篮”和“三步上篮”的命中率均为![]() .假设小华不放弃任何一次投篮机会且每次投篮是否命中相互独立.
.假设小华不放弃任何一次投篮机会且每次投篮是否命中相互独立.
(1)求小华同学两项测试均合格的概率;
(2)设测试过程中小华投篮次数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,![]() φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0
φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0![]() ,﹣2),
,﹣2),
(1)若函数f(x)的最小正周期为π,求函数f(x)的解析式;
(2)当x∈(x0,x0![]() )时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[
)时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[![]() ,
,![]() ]上有且仅有一解,求实数a的取值范围.
]上有且仅有一解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
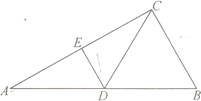

如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题14分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.
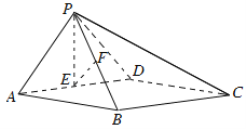
(Ⅰ)求证:PE⊥BC;
(Ⅱ)求证:平面PAB⊥平面PCD;
(Ⅲ)求证:EF∥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com