
【题目】已知函数f(x)=sin2ωx﹣ ![]() (ω>0)的周期为
(ω>0)的周期为 ![]() ,若将其图象沿x轴向右平移a个单位(a>0),所得图象关于原点对称,则实数a的最小值为( )
,若将其图象沿x轴向右平移a个单位(a>0),所得图象关于原点对称,则实数a的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:∵f(x)=sin2(ωx)﹣ ![]()
= ![]() ﹣
﹣ ![]()
=﹣ ![]() cos2ωx,
cos2ωx,
∴ ![]() =
= ![]() ,解得:ω=2,
,解得:ω=2,
∴f(x)=﹣ ![]() cos4x,
cos4x,
∵将函数f(x)图象沿x轴向右平移a个单位(a>0),得到的新函数为g(x)=﹣ ![]() cos(4x﹣4a),
cos(4x﹣4a),
∴cos4a=0,
∴4a=kπ+ ![]() ,k∈Z,
,k∈Z,
当k=0时,a的最小值为 ![]() .
.
故选:D.
【考点精析】认真审题,首先需要了解函数y=Asin(ωx+φ)的图象变换(图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象).
的图象).


科目:高中数学 来源: 题型:
【题目】如图是函数 ![]() 图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
图象的一部分.为了得到这个函数的图象,只要将y=sinx(x∈R)的图象上所有的点( )
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() ,纵坐标不变
,纵坐标不变
B.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() ,纵坐标不变
,纵坐标不变
D.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S= ![]() .已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为 .
.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为 . 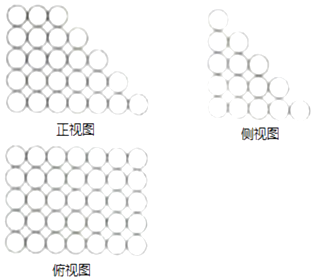
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+2)x+alnx,其中常数a>0. (Ⅰ)当a>2时,求函数f(x)的单调递增区间;
(Ⅱ)设定义在D上的函数y=h(x)在点P(x0 , h(x0))处的切线方程为l:y=g(x),若 ![]() >0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=h(x)的“类对称点”.当a=4时,试问y=f(x)是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下.执行下面的程序框图,则输出的S表示的是( ) 
A.小球第10次着地时向下的运动共经过的路程
B.小球第11次着地时向下的运动共经过的路程
C.小球第10次着地时一共经过的路程
D.小球第11次着地时一共经过的路程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(2,0),曲线C的参数方程为 ![]() (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系. (Ⅰ)求曲线C的普通方程和极坐标方程;
(Ⅱ)过点P且倾斜角为 ![]() 的直线l交曲线C于A,B两点,求|AB|.
的直线l交曲线C于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2+ax﹣a)e1﹣x , 其中a∈R. (Ⅰ)求函数f'(x)的零点个数;
(Ⅱ)证明:a≥0是函数f(x)存在最小值的充分而不必要条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com