Question

7．在区间[0，9]内任取两个数，则这两个数的平方和也在[0，9]内的概率为$\frac{π}{36}$．

Answer 1

分析 首先分析题目求这两个数的平方和也在区间[0，9]内的概率，可以联想到用几何的方法求解，利用面积的比值直接求得结果．

解答 解：将取出的两个数分别用x，y表示，则x，y∈[0，9]
要求这两个数的平方和也在区间[0，9]内，即要求0≤x²+y²≤9，
故此题可以转化为求0≤x²+y²≤9在区域 $\left\{\begin{array}{l}{0≤x≤9}\\{0≤y≤9}\end{array}\right.$内的面积比的问题．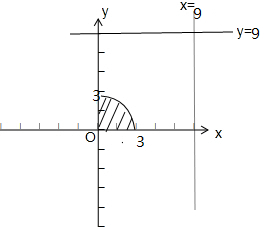

即由几何知识可得到概率为 $\frac{\frac{1}{4}π×9}{{9}^{2}}$=$\frac{π}{36}$；
故答案为：$\frac{π}{36}$．

点评 此题考查等可能时间概率的问题，利用几何概型的方法解决本题，概率知识在高考中难度有所下降，对利用古典概型和几何概型的基本方法要熟练掌握．