
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 上一点,平面
上一点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)若![]() ,试问平面
,试问平面![]() 是否可能与平面
是否可能与平面![]() 垂直?若能,求出
垂直?若能,求出![]() 值;若不能,说明理由。
值;若不能,说明理由。
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a+a﹣1= ![]() (a>1)
(a>1)
(1)求下列各式的值:
(Ⅰ)a ![]() +a
+a ![]() ;
;
(Ⅱ)a ![]() +a
+a ![]() ;
;
(2)已知2lg(x﹣2y)=lgx+lgy,求loga ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
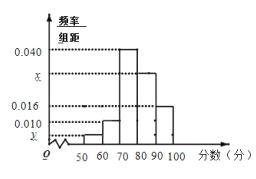
【题目】某重点高中拟把学校打造成新型示范高中,为此制定了学生“七不准”,“一日三省十问”等新的规章制度.新规章制度实施一段时间后,学校就新规章制度随机抽取部分学生进行问卷调查,调查卷共有10个问题,每个问题10分,调查结束后,按分数分成5组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在
,并作出频率分布直方图与样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)在选取的样本中,从分数在70分以下的学生中随机抽取2名学生进行座谈会,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a5=15,数列{bn}满足b1=4,b4=20,且{bn﹣an}(n∈N+)是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com