
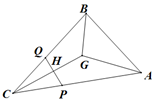
 ИзНјЈ¬ФЪЎчABCЦРЈ¬$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$Ј¬$\overrightarrow{CA}$=$\overrightarrow{a}$Ј¬$\overrightarrow{CB}$=$\overrightarrow{b}$Ј¬ТСЦЄµгPЈ¬Q·Ц±рОЄПЯ¶ОCAЈ¬CBЈЁІ»є¬¶ЛµгЈ©ЙПµД¶ЇµгЈ¬PQУлCGЅ»УЪHЈ¬ЗТHОЄПЯ¶ОCGЦРµгЈ¬Иф$\overrightarrow{CP}$=m$\overrightarrow{a}$Ј¬$\overrightarrow{CQ}$=n$\overrightarrow{b}$Ј¬Фт$\frac{1}{m}$+$\frac{1}{n}$=ЈЁЎЎЎЎЈ©
ИзНјЈ¬ФЪЎчABCЦРЈ¬$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$Ј¬$\overrightarrow{CA}$=$\overrightarrow{a}$Ј¬$\overrightarrow{CB}$=$\overrightarrow{b}$Ј¬ТСЦЄµгPЈ¬Q·Ц±рОЄПЯ¶ОCAЈ¬CBЈЁІ»є¬¶ЛµгЈ©ЙПµД¶ЇµгЈ¬PQУлCGЅ»УЪHЈ¬ЗТHОЄПЯ¶ОCGЦРµгЈ¬Иф$\overrightarrow{CP}$=m$\overrightarrow{a}$Ј¬$\overrightarrow{CQ}$=n$\overrightarrow{b}$Ј¬Фт$\frac{1}{m}$+$\frac{1}{n}$=ЈЁЎЎЎЎЈ©| AЈ® | 2 | BЈ® | 4 | CЈ® | 6 | DЈ® | 8 |
·ЦОц УЙЦШРДµДРФЦКј°ПЯРФФЛЛгЈ¬УГ$\overrightarrow{CA}$Ј¬$\overrightarrow{CB}$Ј¬±нКѕ$\overrightarrow{CH}$Ј¬$\overrightarrow{CH}=\frac{1}{2}\overrightarrow{CG}=\frac{1}{6}ЈЁ\overrightarrow{CA}+\overrightarrow{CB}Ј©$=$\frac{1}{6}ЈЁ\frac{1}{m}\overrightarrow{CA}+\frac{1}{n}\overrightarrow{CB}Ј©=\frac{1}{6m}\overrightarrow{CA}+\frac{1}{6n}\overrightarrow{CB}$Ј¬УЙ$\frac{1}{6m}+\frac{1}{6n}=1$⇒$\frac{1}{m}+\frac{1}{n}=6$Ј®
Ѕвґр ЅвЈєФЪЎчABCЦРЈ¬ЎЯ$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$Ј¬ЎаµгGКЗЎчABCµДЦШРДЈ¬УЙЦШРДµДРФЦКїЙµГ$\overrightarrow{CG}=\frac{2}{3}ЎБ\frac{1}{2}ЎБЈЁ\overrightarrow{CA}+\overrightarrow{CB}Ј©=\frac{1}{3}ЈЁ\overrightarrow{CA}+\overrightarrow{CBЈ©}$
УЦЎЯ$\overrightarrow{CH}=\frac{1}{2}\overrightarrow{CG}=\frac{1}{6}ЈЁ\overrightarrow{CA}+\overrightarrow{CB}Ј©$=$\frac{1}{6}ЈЁ\frac{1}{m}\overrightarrow{CA}+\frac{1}{n}\overrightarrow{CB}Ј©=\frac{1}{6m}\overrightarrow{CA}+\frac{1}{6n}\overrightarrow{CB}$Ј¬
ЎЯИэµгPЈ¬QЈ¬H№ІПЯЈ¬Ўа$\frac{1}{6m}+\frac{1}{6n}=1$⇒$\frac{1}{m}+\frac{1}{n}=6$Ј¬
№КСЎЈєC
µгЖА їјІйПтБїПЯРФФЛЛгЈ¬№ІПЯПтБї»щ±ѕ¶ЁАнЈ¬ЦШРДµДРФЦКЈ¬ПтБїКэіЛµДјёєОТвТеЈ¬КфУЪЦРµµМвЈ®


 ГыРЈїОМГПµБРґр°ё
ГыРЈїОМГПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
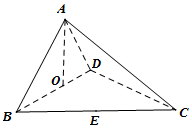 ИзНјЈ¬ФЪИэАвЧ¶A-BCDЦРЈ¬OЎўE·Ц±рОЄBDЎўBCЦРµгЈ¬CA=CB=CD=BD=4Ј¬AB=AD=2$\sqrt{2}$
ИзНјЈ¬ФЪИэАвЧ¶A-BCDЦРЈ¬OЎўE·Ц±рОЄBDЎўBCЦРµгЈ¬CA=CB=CD=BD=4Ј¬AB=AD=2$\sqrt{2}$Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
| AЈ® | 6 | BЈ® | 12 | CЈ® | 24 | DЈ® | 48 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com