
【题目】如图,已知在算法中“![]() ”和“
”和“![]() ”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入![]() ,则输出的
,则输出的![]() ( )
( )![]()

A.3B.4C.5D.6
【答案】B
【解析】
首先读懂程序,输入任意一个无重复数字的三位数,将其个位,十位,百位重新排列,组成一个最大数和一个最小数,写出每次循环的结果,使差是495结束循环,即可得出答案.
先读懂程序:输入任意一个无重复数字的三位数,
将其个位,十位,百位重新排列,组成一个最大数和一个最小数,
然后作差,若差不为495,则继续此过程,经过有限次步骤之后,最后结果一定是495.
对于输入的325,第一次循环:
重新排列后,最大数为532,最小数为235,相减得297,然后![]() ;
;
第二次循环:重新排列后,最大数为972,最小数为279,相减得693,然后![]() ;
;
第三次循环:重新排列后,最大数为963,最小数为369,相减得594,然后![]() ;
;
第四次循环:重新排列后,最大数为954,最小数为459,相减得495,然后![]() ,
,
结束循环,
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
| |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 | |
天数 | 6 | 14 | 18 | 27 | 25 | 20 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率.
的天数中任取3天,求这3天中空气质量至少有2天为优的概率.
(2)已知某企业每天因空气质量造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为
假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
,9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
(i)记该企业9月每天因空气质量造成的经济损失为![]() 元,求
元,求![]() 的分布列;
的分布列;
(ii)试问该企业7月、8月、9月这三个月因空气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在算法中“![]() ”和“
”和“![]() ”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入![]() ,则输出的
,则输出的![]() ( )
( )![]()

A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )
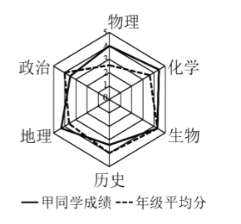
A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,
,![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() ,
,![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() ,以
,以![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,如图所示,山区边界曲线为
,如图所示,山区边界曲线为![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
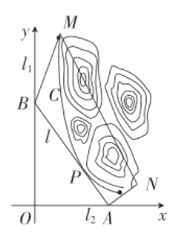
(1)设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() 两点,若公路
两点,若公路![]() 的斜率为-1,求
的斜率为-1,求![]() 的长;
的长;
(2)当公路![]() 的长度最短时,设公路
的长度最短时,设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,并测得四边形
两点,并测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com