
【题目】已知椭圆![]()
![]()
![]() 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】3名志愿者在10月1号至10月5号期间参加社区服务工作.
(1)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记![]() 表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
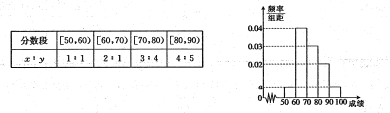
【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,
之比如下表所示,
求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位: ![]() )满足关系
)满足关系![]() ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值。
达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
经计算![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
A.有99.5%的把握认为使用智能手机对学习有影响
B.有99.5%的把握认为使用智能手机对学习无影响
C.有99.9%的把握认为使用智能手机对学习有影响
D.有99.9%的把握认为使用智能手机对学习无影响
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com