函数f(x)=x2+|x-a|-1
(1)若a=0,则方程f(x)=0的解为 .
(2)若函数f(x)有两个零点,则a的取值范围是 .
【答案】
分析:(1)若a=0,解方程 x
2+|x|-1=0,解得|x|的值,即可得到方程f(x)=0的解.
(2)由题意可得函数y=x
2-1的图象 与函数y=-|x-a|的图象有两个交点,当-1≤a≤1 时,结合图象可得满足条件.
当当y=-|x-a|的图象(两条射线)与函数y=x
2-1的图象相切时,求得a=-

,或a=

,结合图象可得a的取值范围.
解答: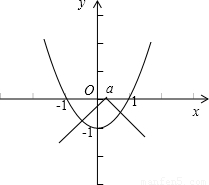
解:(1)若a=0,则方程f(x)=0即 x
2+|x|-1=0,解得|x|=
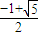
.
∴x=
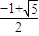
,或 x=
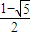
,
故答案为 x=
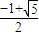
,或 x=
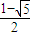
.
(2)由于f(x)=x
2+|x-a|-1=0有两个零点,故函数y=x
2-1的图象 与函数y=-|x-a|的图象有两个交点.
如图所示:
当-1≤a≤1 时,显然函数y=x
2-1的图象 与函数y=-|x-a|的图象有两个交点.
当y=-|x-a|的图象(两条射线)与函数y=x
2-1的图象相切时,
有
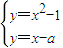
有唯一解,或
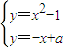
有唯一解.
故 x
2+x-a-1=0 有唯一解,或 x
2-x+a-1=0 有唯一解.
△
1=1+4a+4=0,或△
2=1-4a+4=0. 解得 a=-

,或a=

.
结合图象可得-

<a<

,
故答案为 (-

,

).
点评:本题主要考查函数的零点与方程的根的关系,带有绝对值的函数,体现了化归与转化的数学思想,属于中档题.

 ,或a=
,或a= ,结合图象可得a的取值范围.
,结合图象可得a的取值范围. 解:(1)若a=0,则方程f(x)=0即 x2+|x|-1=0,解得|x|=
解:(1)若a=0,则方程f(x)=0即 x2+|x|-1=0,解得|x|=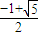 .
.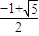 ,或 x=
,或 x=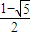 ,
,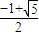 ,或 x=
,或 x=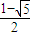 .
.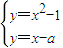 有唯一解,或
有唯一解,或 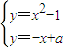 有唯一解.
有唯一解. ,或a=
,或a= .
. <a<
<a< ,
, ,
, ).
).

 阅读快车系列答案
阅读快车系列答案