
【题目】下表是某厂生产某种产品的过程中记录的几组数据,其中![]() 表示产量(单位:吨),
表示产量(单位:吨),![]() 表示生产中消耗的煤的数量(单位:吨).
表示生产中消耗的煤的数量(单位:吨).
|
|
|
|
|
|
|
|
|
|
|
|
(1)试在给出的坐标系下作出散点图,根据散点图判断,在![]() 与
与![]() 中,哪一个方程更适合作为变量
中,哪一个方程更适合作为变量![]() 关于
关于![]() 的回归方程模型?(给出判断即可,不需要说明理由)
的回归方程模型?(给出判断即可,不需要说明理由)
(2)根据(1)的结果以及表中数据,建立变量![]() 关于
关于![]() 的回归方程.并估计生产
的回归方程.并估计生产![]() 吨产品需要准备多少吨煤.参考公式:
吨产品需要准备多少吨煤.参考公式: .
.
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如下表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 | 1.1 | 1.5 | 1.8 | 2.2 | 2.4 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
(参考公式:
![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个直角三角形的三个顶点分别在底面棱长为2的正三棱柱的侧棱上,则该直角三角形斜边的最小值为__________.
【答案】![]()
【解析】 如图,不妨设
如图,不妨设![]() 在
在![]() 处,
处, ![]() ,
,
则有![]() 由
由![]()
![]() 该直角三角形斜边
该直角三角形斜边![]()
故答案为![]() .
.
【题型】填空题
【结束】
16
【题目】已知函数f(x)=![]() ,g(x)=
,g(x)=![]() ,若函数y=f(g(x))+a有三个不同的零点x1,x2,x3(其中x1<x2<x3),则2g(x1)+g(x2)+g(x3)的取值范围为______.
,若函数y=f(g(x))+a有三个不同的零点x1,x2,x3(其中x1<x2<x3),则2g(x1)+g(x2)+g(x3)的取值范围为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次考试共有10道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有7道题的答案是正确的,其余题中:有一道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.试求出该考生:
(Ⅰ)得50分的概率;
(Ⅱ)所得分数![]() 的数学期望(用小数表示,精确到0.01k^s*5#u)
的数学期望(用小数表示,精确到0.01k^s*5#u)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  (a>0,且a≠1)的图象上关于y轴对称的点至少有5对,则实数a的取值范围是( )
(a>0,且a≠1)的图象上关于y轴对称的点至少有5对,则实数a的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( ) 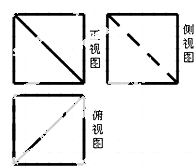
A.54
B.162
C.54+18 ![]()
D.162+18 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com