
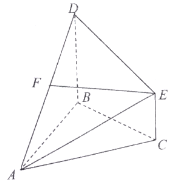
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.
(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取AB中点为O,连接OC、OF,证明四边形OCEF为平行四边形,EF∥OC,然后证明EF∥平面ABC;
(2)以O为坐标原点,分别以![]() 、
、![]() 、
、![]() 的方向为x、y、z轴正方向,建立空间直角坐标系.不妨令正三角形ABC的边长为2,求出相关的的坐标,求出平面AEC的法向量,平面AED的法向量,取法向量的方向一进一出,利用空间向量的公式求解即可.
的方向为x、y、z轴正方向,建立空间直角坐标系.不妨令正三角形ABC的边长为2,求出相关的的坐标,求出平面AEC的法向量,平面AED的法向量,取法向量的方向一进一出,利用空间向量的公式求解即可.
(1)证明:取AB中点为O,连接OC、OF,∵O、F分别为AB、AD中点,
∴OF∥BD且BD=2OF,又CE∥BD且BD=2CE,∴CE∥OF且CE=OF,∴四边形OCEF为平行四边形,∴EF∥OC,
又OC平面ABC且EF平面ABC,∴EF∥平面ABC.
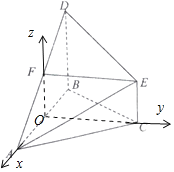
(2)∵三角形ABC为等边三角形,O为AB中点,∴OC⊥AB,∵平面ABC⊥平面ABD且平面ABC∩平面ABD=AB,
又BD⊥AB且BD平面ABD,∴BD⊥平面ABC,又OF∥BD,∴OF⊥平面ABC,
以O为坐标原点,分别以![]() 、
、![]() 、
、![]() 的方向为x、y、z轴正方向,建立空间直角坐标系.
的方向为x、y、z轴正方向,建立空间直角坐标系.
不妨令正三角形ABC的边长为2,则O(0,0,0),A(1,0,0),![]() ,
,![]() ,D(﹣1,0,2),
,D(﹣1,0,2),
∴![]() ,
,![]() ,
,![]() 设平面AEC的法向量为
设平面AEC的法向量为![]() ,则
,则 ,
,
不妨令![]() ,则
,则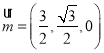 ,
,
设平面AED的法向量为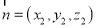 ,
,
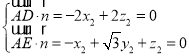 令
令![]()
得![]() ,
,
∴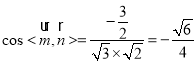 ,
,
∴所求二面角C﹣AE﹣D的余弦值为![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】数列![]() 满足
满足![]() .
.
①存在![]() 可以生成的数列
可以生成的数列![]() 是常数数列;
是常数数列;
②“数列![]() 中存在某一项
中存在某一项![]() ”是“数列
”是“数列![]() 为有穷数列”的充要条件;
为有穷数列”的充要条件;
③若![]() 为单调递增数列,则
为单调递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
④只要![]() ,其中
,其中![]() ,则
,则![]() 一定存在;
一定存在;
其中正确命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,C、D两点的坐标为
为坐标原点,C、D两点的坐标为![]() ,曲线
,曲线![]() 上的动点P满足
上的动点P满足![]() .又曲线
.又曲线![]() 上的点A、B满足
上的点A、B满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点A在第一象限,且![]() ,求点A的坐标;
,求点A的坐标;
(3)求证:原点到直线AB的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列 ![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
, ![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为数列
为数列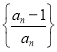 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(1)求![]() 的值;
的值;
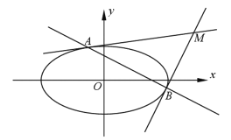
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲乙两地相距100海里,船从甲地匀速驶到乙地,已知某船的最大船速是36海里/时:当船速不大于每小时30海里/时,船每小时使用的燃料费用和船速成正比;当船速不小于每小时30海里/时,船每小时使用的燃料费用和船速的平方成正比;当船速为30海里/时,它每小时使用的燃料费用为300元;其余费用(不论船速为多少)都是每小时480元;
(1)试把每小时使用的燃料费用P(元)表示成船速v(海里/时)的函数;
(2)试把船从甲地行驶到乙地所需要的总费用Y表示成船速v的函数;
(3)当船速为每小时多少海里时,船从甲地到乙地所需要的总费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com