
【题目】已知在平面直角坐标系xOy中,曲线C的参数方程为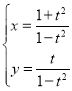 (t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(
(t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(![]() )
)![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)若直线l交曲线C于A,B两点,交x轴于点P,求![]() 的值.
的值.
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】我国全面二孩政策已于2016年1月1日起正式实施.国家统计局发布的数据显示,从2012年到2017年,中国的人口自然增长率变化始终不大,在5‰上下波动(如图).

为了了解年龄介于24岁至50岁之间的适孕夫妻对生育二孩的态度如何,统计部门按年龄分为9组,每组选取150对夫妻进行调查统计有生育二孩意愿的夫妻数,得到下表:
年龄区间 |
|
|
|
|
|
|
|
|
|
有意愿数 | 80 | 81 | 87 | 86 | 84 | 83 | 83 | 70 | 66 |
(1)设每个年龄区间的中间值为![]() ,有意愿数为
,有意愿数为![]() ,求样本数据的线性回归直线方程,并求该模型的相关系数
,求样本数据的线性回归直线方程,并求该模型的相关系数![]() (结果保留两位小数);
(结果保留两位小数);
(2)从![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
这五个年龄段中各选出一对夫妻(能代表该年龄段超过半数夫妻的意愿)进一步调研,再从这5对夫妻中任选2对夫妻.求其中恰有一对不愿意生育二孩的夫妻的概率.
(参考数据和公式: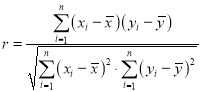 ,
,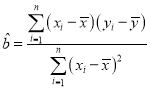 ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中华人民共和国的国旗是五星红旗,旗面左上方缀着五颗黄色五角星,四颗小星环拱在一颗大星之后,并各有一个角尖正对大星的中心点,象征着中国共产党领导下的革命人民大团结和中国人民对党的衷心拥护.五角星可以通过正五边形连接对角线得到,如图所示,在正五边形ABCDE内部任取一点,则该点取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的中a1=1,a2=2,且满足![]() .
.
(1)求数列{an}的通项公式;
(2)设bn![]() ,记数列{bn}的前n项和为Tn,若|Tn+1|
,记数列{bn}的前n项和为Tn,若|Tn+1|![]() ,求n的最小值.
,求n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将字母![]() 放入
放入![]() 的方表格,每个格子各放一个字母,则每一行的字母互不相同,每一列的字母也互不相同的概率为_______;若共有
的方表格,每个格子各放一个字母,则每一行的字母互不相同,每一列的字母也互不相同的概率为_______;若共有![]() 行字母相同,则得k分,则所得分数
行字母相同,则得k分,则所得分数![]() 的数学期望为______;(注:横的为行,竖的为列;比如以下填法第二行的两个字母相同,第1,3行字母不同,该情况下
的数学期望为______;(注:横的为行,竖的为列;比如以下填法第二行的两个字母相同,第1,3行字母不同,该情况下![]() )
)
a | b |
c | c |
a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”逐渐成为人们支付购物的一种形式.某机构对“使用微信支付”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信支付”赞成人数如下表.
年龄 (单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信支付”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
的被调查人中按照赞成与不赞成分层抽样,抽取5人进行追踪调查,在5人中抽取3人做专访,求3人中不赞成使用微信支付的人数的分布列和期望值.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,已知点P为侧面
中,已知点P为侧面![]() 上的一动点,则下列结论正确的是( )
上的一动点,则下列结论正确的是( )
A.若点P总保持![]() ,则动点P的轨迹是一条线段;
,则动点P的轨迹是一条线段;
B.若点P到点A的距离为![]() ,则动点P的轨迹是一段圆弧;
,则动点P的轨迹是一段圆弧;
C.若P到直线![]() 与直线
与直线![]() 的距离相等,则动点P的轨迹是一段抛物线;
的距离相等,则动点P的轨迹是一段抛物线;
D.若P到直线![]() 与直线
与直线![]() 的距离比为
的距离比为![]() ,则动点P的轨迹是一段双曲线.
,则动点P的轨迹是一段双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“九儿问甲歌”就是其中一首:“一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七,借问长儿多少岁,各儿岁数要详推.”这首歌决的大意是:“一位老公公有九个儿子,九个儿子从大到小排列,相邻两人的年龄差三岁,并且儿子们的年龄之和为207岁,请问大儿子多少岁,其他几个儿子年龄如何推算.”在这个问题中,记这位公公的第![]() 个儿子的年龄为
个儿子的年龄为![]() ,则
,则![]() ( )
( )
A.17B.29C.23D.35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com