
【题目】![]() 是直线
是直线![]() 与函数
与函数![]() 图像的两个相邻的交点,且
图像的两个相邻的交点,且![]() .
.
(1)求![]() 的值和函数
的值和函数![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象上各点的横坐标伸长为原来的
的图象上各点的横坐标伸长为原来的![]() 倍(纵坐标不变),再将得到的图象向左平移
倍(纵坐标不变),再将得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 的对称轴方程.
的对称轴方程.
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为D,若对于任意的x1 , x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x3+sinx+2的某一个对称中心,并利用对称中心的上述定义,可得到 ![]() …
… ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线![]() 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线![]() .(1)求曲线
.(1)求曲线![]() 的普通方程;(2)若点
的普通方程;(2)若点![]() 在曲线
在曲线![]() 上,点
上,点![]()
![]() ,当点
,当点![]() 在曲线
在曲线![]() 上运动时,求
上运动时,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣2|x﹣1|.
(1)解不等式f(x)≥﹣2;
(2)对任意x∈R,都有f(x)≤x﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx+1. (Ⅰ)设ω为大于0的常数,若f(ωx)在区间 ![]() 上单调递增,求实数ω的取值范围;
上单调递增,求实数ω的取值范围;
(Ⅱ)设集合 ![]() ,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围.
,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c且b=c,∠A的平分线为AD,若 ![]() =m
=m ![]()
![]() .
.
(1)当m=2时,求cosA
(2)当 ![]() ∈(1,
∈(1, ![]() )时,求实数m的取值范围.
)时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项为正的数列{an}是等比数列,a1=2,a5=32,数列{bn}满足:对于任意n∈N* , 有a1b1+a2b2+…+anbn=(n﹣1)2n+1+2.
(1)求数列{an}的通项公式;
(2)令f(n)=a2+a4+…+a2n , 求 ![]() 的值;
的值;
(3)求数列{bn}通项公式,若在数列{an}的任意相邻两项ak与ak+1之间插入bk(k∈N*)后,得到一个新的数列{cn},求数列{cn}的前100项之和T100 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD满足AD∥BC,BA=AD=DC= ![]() BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点.
BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F,G分别为B1D,AE的中点. 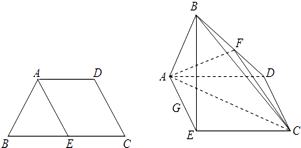
(1)求三棱锥E﹣ACB1的体积;
(2)证明:B1E∥平面ACF;
(3)证明:平面B1GD⊥平面B1DC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com