
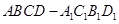 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱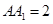 ,为
,为 中点,
中点, 为
为 中点,
中点,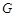 为
为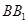 上一个动点.
上一个动点.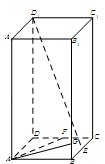
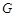 点的位置,使得
点的位置,使得 ;
; 时,求二面角
时,求二面角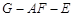 的平
的平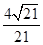
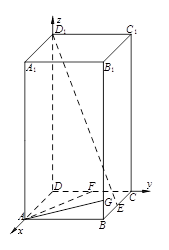
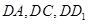 所在直线为
所在直线为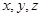 轴建立空间直角坐标系
轴建立空间直角坐标系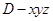 ,则
,则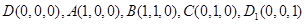
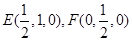 ………………2分
………………2分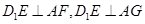 ,设
,设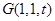
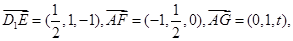
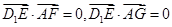 得
得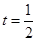 ,
,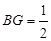 ,得
,得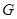 为
为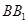 的四等分点.………………………6分
的四等分点.………………………6分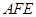 的一个法向量为
的一个法向量为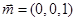 ,设平面
,设平面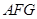 的法向量为
的法向量为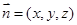
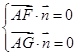 ,得
,得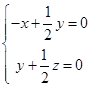 ,取
,取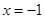 ,得
,得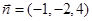 , ……………10分
, ……………10分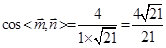 ,∴二面角
,∴二面角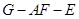 的平面角余弦值为
的平面角余弦值为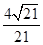 .12分
.12分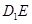 在平面
在平面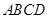 内的射影为
内的射影为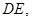 ,且四边形
,且四边形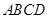 为正方形,
为正方形,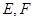 为中点, ∴
为中点, ∴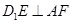
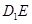 在平面
在平面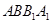 内的射影为
内的射影为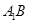 ,则
,则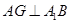
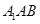 ~△
~△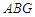 , ∴
, ∴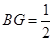 ,得
,得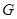 为
为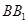 的四等分点. …………………6分
的四等分点. …………………6分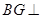 平面
平面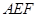 ,过
,过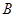 点作
点作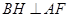 ,垂足为
,垂足为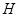 ;
; ,则
,则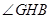 为二面角
为二面角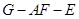 的平面角;…………………………8分
的平面角;…………………………8分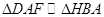 ,得
,得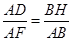 ,解得
,解得
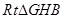 中,
中,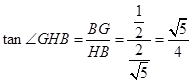 ,
,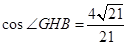 ;∴二面角
;∴二面角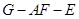 的平面角余弦值为
的平面角余弦值为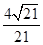 . …12分
. …12分

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源:不详 题型:填空题
 平面ABC,
平面ABC, ,给出下列结论:①
,给出下列结论:① ;②平面
;②平面 平面PBC;③直线
平面PBC;③直线 平面PAE;④
平面PAE;④ ;⑤直线PD与平面PAB所成角的余弦值为
;⑤直线PD与平面PAB所成角的余弦值为 。
。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
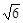 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记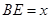 ,用
,用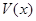 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.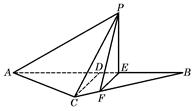
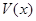 的表达式;
的表达式;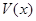 取得最大值?
取得最大值?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,给定以下条件:
,给定以下条件: 内不共线的三点到
内不共线的三点到 的距离相等;②
的距离相等;② 是
是 内的两条直线,且
内的两条直线,且 ;
; 是两条异面直线,且
是两条异面直线,且 ;
; 的是( )
的是( )| A.① | B.② | C.①③ | D.③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
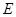 是
是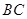 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持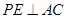 .则动点
.则动点 的轨迹与△
的轨迹与△ 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )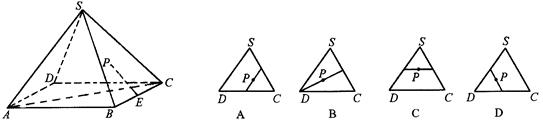
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com