
【题目】阶梯水价的原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制订合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,得到数据如下(单位:吨).
郊区:19 25 28 32 34
城区:18 19 21 22 22 23 23 23 24 25 26 27 28 28 28 29 29 31 35 42
(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为1:5,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一阶梯的居民用户用水价格保持不变,试根据样本总体的思想,分析此方案是否符合国家“保基本”政策.
科目:高中数学 来源: 题型:
【题目】某班有20人参加语文、数学考试各一次,考试按10分制评分,即成绩是0到10的整数.考试结果是:(1)没有0分;(2)没有两个同学的语文、数学成绩都相同.我们说“同学![]() 比
比![]() 的成绩好”是指“同学
的成绩好”是指“同学![]() 的语文、数学成绩都不低于
的语文、数学成绩都不低于![]() ”.证明:存在三个同学
”.证明:存在三个同学![]() 、
、![]() 、
、![]() ,使得同学
,使得同学![]() 比
比![]() 的成绩好,同学
的成绩好,同学![]() 比
比![]() 的成绩好.
的成绩好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:

该函数模型如下:

根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
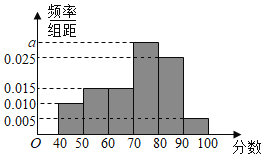
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于![]() .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的左顶点
的左顶点![]() 为圆心作圆
为圆心作圆![]() :
:![]() ,设圆
,设圆![]() 与椭圆
与椭圆![]() 交于点
交于点![]() 与点
与点![]() .
.
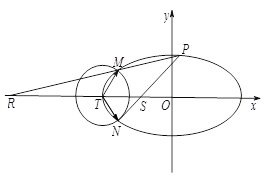
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(3)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,且直线
的任意一点,且直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() 为坐标原点,
为坐标原点,
求证:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com