
知数列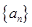 的首项
的首项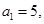 前
前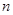 项和为
项和为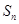 ,且
,且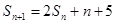
(1)证明:数列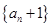 是等比数列;
是等比数列;
(2)令 ,求函数
,求函数 在点
在点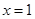 处的导数
处的导数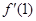 ,并比较
,并比较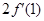 与
与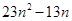 的大小.
的大小.
(1)详见解析;(2)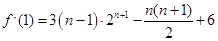 ; 当
; 当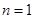 时,
时,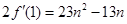 ; 当
; 当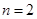 时,
时,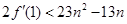 ;当
;当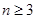 时,
时,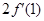
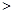
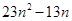 .
.
解析试题分析:(1)先利用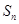 与
与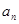 的递推关系得到
的递推关系得到 与
与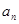 的递推关系式,再通过构造新数列,并结合等比数列的定义来证明
的递推关系式,再通过构造新数列,并结合等比数列的定义来证明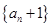 是等比数列;(2)先求导得到
是等比数列;(2)先求导得到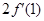 的表达式,然后分组求和,一部分是用错位相减法,另一部分是用等差数列求和公式,最后通过作差比较
的表达式,然后分组求和,一部分是用错位相减法,另一部分是用等差数列求和公式,最后通过作差比较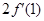 与
与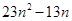 的大小情况.
的大小情况.
试题解析:(1)由已知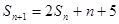 ,可得
,可得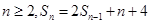 两式相减得
两式相减得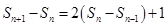 即
即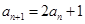 从而
从而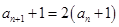 4分
4分
当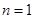 时
时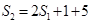 所以
所以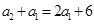 又
又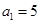 所以
所以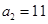 从而
从而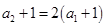 5分
5分
故总有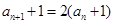 ,
,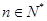 又
又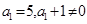
从而 即数列
即数列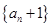 是等比数列; 6分
是等比数列; 6分
(2)由(1)知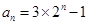 ,因为
,因为 所以
所以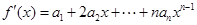
从而 =
=
=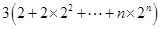
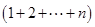
令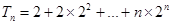 ,
,
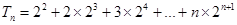
错位相减得,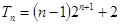
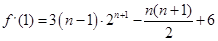 10分
10分
由上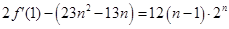
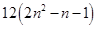 =
=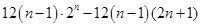 =12
=12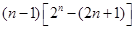 ①
①
当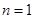 时,①式=0所以
时,①式=0所以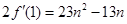 ;
;
当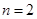 时,①式=12
时,①式=12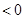 所以
所以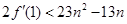
当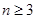 时,
时,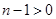 又由函数
又由函数 可
可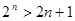
所以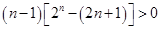 即①
即①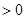 从而
从而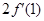
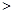
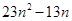 14分
14分
考点:1、数列通项公式的求法,2、数列前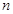 项和的求法,3、函数的求导.
项和的求法,3、函数的求导.


科目:高中数学 来源: 题型:解答题
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少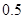 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列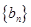 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
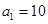 | 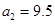 | 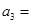 | 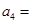 | |
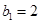 |   3 3 | 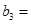 | 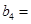 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com