
【题目】已知函数f(x)=ln(2+x),g(x)=ln(2﹣x)
(1)判断函数h(x)=f(x)﹣g(x)的奇偶性;
(2)求使f(x)≥g(x)成立的x的取值范围.
【答案】
(1)解:函数h(x)=f(x)﹣g(x)=ln(2+x)﹣ln(2﹣x)
由 ![]() 知﹣2<x<2
知﹣2<x<2
∴函数y=f(x)﹣g(x)的定义域为(﹣2,2)h(﹣x)=ln(2﹣x)﹣ln(2+x)=﹣h(x)∴h(x)为奇函数
(2)解:由f(x)≥g(x)得ln(2+x)≥ln(2﹣x)
∴ 
解得0≤x<2
∴使f(x)≥g(x)成立的x的取值范围是[0,2)
【解析】(1)求出函数的定义域,然后判断函数的奇偶性.(2)直接利用对数不等式化简求解即可.
【考点精析】关于本题考查的奇偶性与单调性的综合,需要了解奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能得出正确答案.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设H:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算的K2≈3.918,经查临界值表知P(K2≥3.841)≈0.05.则下列表述中正确的是( )
A.有95℅的把握认为“这种血清能起到预防感冒的作用”
B.若有人未使用该血清,那么他一年中有95℅的可能性得感冒
C.这种血清预防感冒的有效率为95℅
D.这种血清预防感冒的有效率为5℅
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个命题:
①函数f(x)= ![]() x﹣lnx(x>0),则y=f(x)在区间(
x﹣lnx(x>0),则y=f(x)在区间( ![]() ,1)内无零点,在区间(1,e)内有零点;
,1)内无零点,在区间(1,e)内有零点;
②函数f(x)=log2(x+ ![]() ),g(x)=1+
),g(x)=1+ ![]() 不都是奇函数;
不都是奇函数;
③若函数f(x)满足f(x﹣1)=﹣f(x+1),且f(1)=2,则f(7)=﹣2;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则x1x2=1,
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年一月份推出新产品A,其成本价为492元/件,经试销调查,销售量与销售价的关系如下表:
销售价(x/元件) | 650 | 662 | 720 | 800 |
销售量(y件) | 350 | 333 | 281 | 200 |
由此可知,销售量y(件)与销售价x(元/件)可近似看作一次函数y=kx+b的关系(通常取表中相距较远的两组数据所得一次函数较为精确).
(1)写出以x为自变量的函数y的解析式及定义域;
(2)试问:销售价定为多少时,一月份销售利润最大?并求最大销售利润和此时的销售量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算
(1)计算27 ![]() +lg5﹣2log23+lg2+log29.
+lg5﹣2log23+lg2+log29.
(2)已知f(x)=3x2﹣5x+2,求f( ![]() )、f(﹣a)、f(a+3).
)、f(﹣a)、f(a+3).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是
A.命题“对![]() ,都有
,都有![]() ”的否定为“
”的否定为“![]() ,使得
,使得![]() ”
”
B.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
C. “若![]() ,则
,则![]() ” 是真命题
” 是真命题
D.甲、乙两位学生参与数学模拟考试,设命题![]() 是“甲考试及格”,
是“甲考试及格”,![]() 是“乙考试及格”,则命题“至少有一位学生不及格”可表示为
是“乙考试及格”,则命题“至少有一位学生不及格”可表示为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知A为左顶点,F是左焦点,l交OA的延长线于点B,点P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是① ![]() ; ②
; ② ![]() ; ③
; ③ ![]() ; ④
; ④ ![]() ; ⑤
; ⑤ ![]() 其中正确的是( )
其中正确的是( )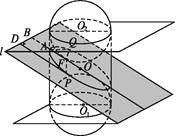
A.①②
B.①③④
C.②③⑤
D.①②③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ ![]() 或x>﹣
或x>﹣ ![]() }
}
C.{x|﹣ ![]() <x<﹣
<x<﹣ ![]() }
}
D.{x|﹣3<x<﹣2}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com