
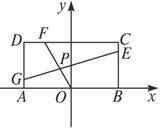
已知常数a>0,在矩形ABCD中,AB=4,BC=4a,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且![]() =
=![]() =
=![]() ,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
,P为GE与OF的交点(如图).问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由.
剖析:根据题设条件首先求出P点坐标满足的方程,据此可判断是否存在两点,使得点P到两定点距离的和为定值.
解:按题意,有A(-2,0),B(2,0),C(2,4a),D(-2,4a).
设![]() =
=![]() =
=![]() =k(0≤k≤1),由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
=k(0≤k≤1),由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为2ax+(2k-1)y=0. ①
直线GE的方程为-a(2k-1)x+y-2a=0. ②
由①②消去参数k,得点P(x,y)满足方程2a2x2+y2-2ay=0.
整理得![]() +
+![]() =1.
=1.
当a2=![]() 时,点P的轨迹为圆弧,所以不存在符合题意的两点.
时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当a2≠![]() 时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
时,点P的轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
当a2<![]() 时,点P到椭圆两个焦点(-
时,点P到椭圆两个焦点(-![]() ,a),(
,a),(![]() ,a)的距离之和为定值2.
,a)的距离之和为定值2.
当a2>![]() 时,点P到椭圆两个焦点(0,a-
时,点P到椭圆两个焦点(0,a-![]() ),(0,a+
),(0,a+![]() )的距离之和为定值2a.
)的距离之和为定值2a.
讲评:本题主要考查根据已知条件求轨迹的方法,椭圆的方程和性质,利用方程判定曲线的性质,曲线与方程关系等解析几何的基本思想和综合解题能力.在解题过程中蕴涵着方程思想、分类讨论思想和构造法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| b |
| a |
| 5 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)已知函数![]() (x>0)在x = 1处
(x>0)在x = 1处
取得极值–3–c,其中a,b,c为常数。
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式![]() 恒成立,求c的取值范围。
恒成立,求c的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() (x>0)在x = 1处取得极值
(x>0)在x = 1处取得极值![]() ,其中a,b,c为常数。(1)试确定a,b的值; (2)讨论函数f(x)的单调区间;
,其中a,b,c为常数。(1)试确定a,b的值; (2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式![]() 恒成立,求c的取值范围。
恒成立,求c的取值范围。
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试理科数学卷(重庆) 题型:解答题
(本小题满分13分)已知函数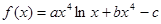 (x>0)在x = 1处取得极值–3–c,其中a,b,c为常数。
(x>0)在x = 1处取得极值–3–c,其中a,b,c为常数。
(1)试确定a,b的值;(6分)
(2)讨论函数f(x)的单调区间;(4分)
(3)若对任意x>0,不等式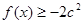 恒成立,求c的取值范围。(3分)
恒成立,求c的取值范围。(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com