
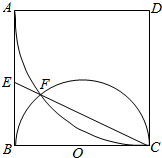
 如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于C,F,连接CF并延长交AB于点E.
如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于C,F,连接CF并延长交AB于点E.分析 (1)根据∠CDO=∠FDO,BC是的切线,且CF是圆D的弦,得到$∠BCE=\frac{1}{2}∠CDF$,即∠CDO=∠BCE,得到两个三角形全等,得到线段相等,得到结论.
(2)根据两个角对应相等,得到两个三角形相似,得到对应边成比例,根据所给的长度,代入比例式,得到要求的线段.然后利用勾股定理在直角三角形BFE中求EF即可.
解答 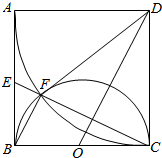 (1)证明:连接DF,DO,则∠CDO=∠FDO,
(1)证明:连接DF,DO,则∠CDO=∠FDO,
因为BC是的切线,且CF是圆D的弦,
所以$∠BCE=\frac{1}{2}∠CDF$,即∠CDO=∠BCE,
故Rt△CDO≌Rt△BCE,
所以EB=OC=$\frac{1}{2}$AB.
所以E是AB的中点.
(2)解:连接BF,
∵∠BEF=∠CEB,∠ABC=∠EFB
∴△FEB∽△BEC,
得$\frac{BF}{BE}=\frac{CB}{CE}$,
∵ABCD是边长为a的正方形,
∴BF=$\frac{\sqrt{5}}{5}$a.
∵BE=$\frac{1}{2}$a,
∴EF=$\sqrt{B{E}^{2}-B{F}^{2}}$=$\sqrt{(\frac{1}{2}a)^{2}-(\frac{\sqrt{5}a}{5})^{2}}$=$\sqrt{\frac{{a}^{2}}{4}-\frac{{a}^{2}}{5}}=\sqrt{\frac{{a}^{2}}{20}}$=$\frac{\sqrt{5}a}{10}$.
点评 本题考查相似三角形的判定和性质,考查圆周角定理,本题解题的关键是得到三角形全等和三角形相似,本题是一个中档题目.


科目:高中数学 来源: 题型:解答题
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 人数 | 2 | 4 | 8 | 4 | 2 |
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 人数 | 1 | 5 | 6 | 5 | 3 |
| 睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
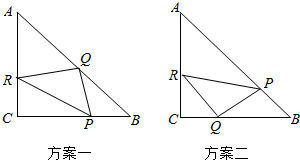 在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案:
在一个直角边长为10m的等腰直角三角形ABC的草地上,铺设一个也是等腰直角三角形PQR的花地,要求P,Q,R三点分别在△ABC的三条边上,且要使△PQR的面积最小,现有两种设计方案:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{10}$ | C. | 3$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com