
【题目】以下结论正确的序号有_________
(1)根据![]() 列联表中的数据计算得出
列联表中的数据计算得出![]() ≥6.635, 而P(
≥6.635, 而P(![]() ≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系.
≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系.
(2)在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关.
(3)在线性回归分析中,相关系数为![]() ,
,![]() 越接近于1,相关程度越大;
越接近于1,相关程度越大;![]() 越小,相关程度越小.
越小,相关程度越小.
(4)在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15.
的值一定是15.
【答案】(1)(3).
【解析】分析:根据独立性检验、残差图、相关系数、回归分析的定义及性质,逐一分析四个答案的真假即可.
详解:对于(1),根据2×2列联表中的数据计算得出![]() ≥6.635, 而P(
≥6.635, 而P(![]() ≥6.635)≈0.01,则有99%的把握认为两个分类变量有关系,故(1)正确.
≥6.635)≈0.01,则有99%的把握认为两个分类变量有关系,故(1)正确.
对于(2),根据残差图的意义可得,当带状区域的宽度较小时,说明选用的模型比价合适,而当带状区域的宽度较大时,说明选用的模型不合适,故(2)不正确.
对于(3),在线性回归分析中,相关系数为r,|r|越接近于1,则相关程度越大;|r|越接近于0,则相关程度越小.故(3)正确.
对于(4),在回归直线y=0.5x85中,当x=200时,y=15,但实际观测值可能不是15,故(4)不正确.
综上可得(1)(3)正确.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(![]() )(A>0,ω>0,
)(A>0,ω>0,![]() )的部分图象如图所示.若横坐标分别为-1、1、5的三点M,N,P都在函数f(x)的图象上,则sin∠MNP的值为( )
)的部分图象如图所示.若横坐标分别为-1、1、5的三点M,N,P都在函数f(x)的图象上,则sin∠MNP的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.
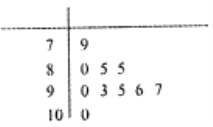
(1)计算这10名学生的成绩的均值和方差;
(2)给出正态分布的数据:P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
由(1)估计从全市随机抽取一名学生的成绩在(76,97)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)同时满足:
①对于定义域上的任意x恒有f(x)+f(﹣x)=0,
②对于定义域上的任意x1,x2,当x1≠x2时,恒有![]() 0,则称函数f(x)为“理想函数”.
0,则称函数f(x)为“理想函数”.
给出下列四个函数中①f(x)![]() ; ②f(x)
; ②f(x)![]() ; ③f(x)
; ③f(x)![]() ;④f(x)
;④f(x)![]() ,
,
能被称为“理想函数”的有_______________(填相应的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点. 
(1)证明B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的正弦值.
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ![]() ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y)且当x>0,f(x)<0.
给出下列四个结论:
①f(0)=0;②f(x)为偶函数;
③f(x)为R上减函数;④f(x)为R上增函数.
其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )
(参考数据:![]() )
)

A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】环保组织随机抽检市内某河流2015年内100天的水质,检测单位体积河水中重金属含量![]() ,并根据抽检数据绘制了如下图所示的频率分布直方图.
,并根据抽检数据绘制了如下图所示的频率分布直方图.
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)假设某企业每天由重金属污染造成的经济损失![]() (单位:元)与单位体积河水中重金属含量
(单位:元)与单位体积河水中重金属含量![]()
的关系式为 ,若将频率视为概率,在本年内随机抽取一天,试估计这天经济损失不超过500元的概率.
,若将频率视为概率,在本年内随机抽取一天,试估计这天经济损失不超过500元的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com