
 ,
, 满足条件
满足条件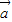 +
+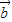 =(0,1),
=(0,1), -
-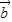 =(-1,2),则
=(-1,2),则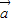 •
•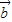 = .
= .  全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:南京一模 题型:填空题
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州中学高三(上)期中数学试卷(解析版) 题型:填空题
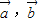 满足|
满足|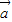 |=1,|
|=1,|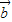 |=2,
|=2,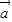 与
与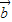 的夹角为
的夹角为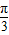 ,以
,以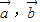 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .查看答案和解析>>
科目:高中数学 来源:2011年江苏省南京外国语学校高三考前适应性测试数学试卷(解析版) 题型:填空题
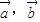 满足|
满足|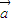 |=1,|
|=1,|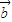 |=2,
|=2,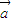 与
与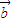 的夹角为
的夹角为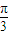 ,以
,以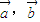 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .查看答案和解析>>
科目:高中数学 来源:2011年江苏省南京市高考数学一模试卷(解析版) 题型:解答题
 满足|
满足| |=1,|
|=1,| |=2,
|=2, 与
与 的夹角为
的夹角为 ,以
,以 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com