Question

平行六面体ABCD-A₁B₁C₁D₁的底面是矩形，侧棱长为2cm，点C₁在底面ABCD上的射影H是CD的中点，CC₁与底面ABCD成60°的角，二面角A-CC₁-D的平面角等于30°，求此平行六面体的表面积．

Answer 1

分析：平行六面体的表面积是各个面的面积和，相对的两个面相同；故由侧棱长为2cm，点C₁在底面ABCD上的射影H是CD的中点，CC₁与底面ABCD成60°的角，可求出侧面CDD₁C₁的面积；由二面角A-CC₁-D的平面角等于30°，可以求出底面边长AD，从而求出底面矩形ABCD的面积和侧面矩形ADD₁A₁的面积；即得此平行六面体的表面积．

解答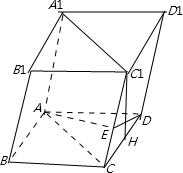：解：如图，在平行六面体 ABCD-A₁B₁C₁D₁中，底面ABCD是矩形，∴CD⊥BC，
又点C₁在底面ABCD上的射影H是CD的中点，
∴C₁H⊥平面ABCD，∴C₁H⊥BC，∴BC⊥平面CDD₁C₁，∴BC⊥CC₁，
∴∠C₁CH是CC₁与底面ABCD成的角，即∠C₁CH=60°；
又CC₁=2，∴C1H=

3

，CH=1，∴CD=2CH=2，
∴?CDD₁C₁的面积为：S₁=CD•C₁H=2×

3

=2

3

；
又由BC∥AD，且BC⊥平面CDD₁C₁，
∴AD⊥平面CDD₁C₁；过点D作DE⊥CC₁，垂足为E，连接AE，则AE⊥CC₁；
∴∠AED是二面角A-CC₁-D的平面角，∴∠AED=30°．
在Rt△AED中，DE=

3

，∠ADE=90°，∴AD=1，
∴矩形ABCD的面积为：S₂=AD•CD=1×2=2，矩形ADD₁A₁的面积为：S₃=AD•DD₁=1×2=2，
所以，平行六面体ABCD-A₁B₁C₁D₁的表面积为：S=2S₁+2S₂+2S₃=4

3

+4+4=8+4

3

．

点评：本题是求多面体的表面积，即各个面的面积和；本题的关键是用好直线与平面所成的角，二面角的平面角．