【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用，从孩子一周岁生日开始，每年到银行储蓄
元一年定期，若年利率为
保持不变，且每年到期时存款（含利息）自动转为新的一年定期，当孩子18岁生日时不再存入，将所有存款（含利息）全部取回，则取回的钱的总数为
A.
B.
C.
D.
科目：高中数学 来源： 题型：
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.下面是以往公司对该产品的宣传费用
(单位：万元)和产品营业额
(单位：万元)的统计折线图.
(Ⅰ)根据折线图可以判断，可用线性回归模型拟合宣传费用
与产品营业额
的关系，请用相关系数加以说明；
(Ⅱ)建立产品营业额
关于宣传费用
的归方程；
(Ⅲ)若某段时间内产品利润
与宣传费
和营业额
的关系为
，应投入宣传费多少万元才能使利润最大，并求最大利润.
参考数据： 
， 
， 
， 
， 
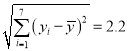参考公式：相关系数，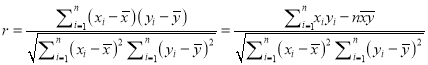 
，
回归方程
中斜率和截距的最小二乘佔计公式分别为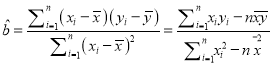
， 
.(计算结果保留两位小数)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图
,在矩形
中, 
, 
为
的中点, 
为
的中点.将
沿
折起到
,使得平面
平面
（如图
）.
图1 图2
（Ⅰ）求证: 
；
（Ⅱ）求直线
与平面
所成角的正弦值；
（Ⅲ）在线段
上是否存在点
,使得
平面
?若存在,求出
的值;若不存在,请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合
是集合
的一个含有
个元素的子集.
（Ⅰ）当
时,
设
（i）写出方程
的解
；
（ii）若方程
至少有三组不同的解,写出
的所有可能取值.
（Ⅱ）证明:对任意一个
,存在正整数
使得方程
至少有三组不同的解.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，中心在原点的椭圆C的上焦点为
，离心率等于
．
求椭圆C的方程；
设过且不垂直于坐标轴的动直线l交椭圆C于A、B两点，问：线段OF上是否存在一点D，使得以DA、DB为邻边的平行四边形为菱形？作出判断并证明．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的首项
， 
， 
．
(1)求证：数列
为等比数列；
(2)记
，若Sn<100，求最大正整数n；
(3)是否存在互不相等的正整数m，s，n，使m，s，n成等差数列，且am－1，as－1，an－1成等比数列？如果存在，请给以证明；如果不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个袋中有
个大小之地都相同的小球，其中红球
个，白球
个，黑球个，现从袋中有放回的取球，每次随机取一个，连续取两次.
（1）设
表示先后两次所取到的球，试写出所有可能抽取结果；
（2）求连续两次都取到白球的概率；
（3）若取到红球记分，取到白球记分，取到黑球记
分，求连续两次球所得总分数大于分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（
）若曲线
在点
处的切线与直线
平行，求
的值．
（
）在（1）的条件下，求函数
的单调区间和极值．
（
）在（1）的条件下，试判断函数
的零点个数，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】微信支付诞生于微信红包，早期知识作为社交的一部分“发红包”而诞生的，在发红包之余才发现，原来微信支付不仅可以用来发红包，还可以用来支付，现在微信支付被越来越多的人们所接受，现从某市市民中随机抽取300为对是否使用微信支付进行调查，得到下列
的列联表：
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据，我们得到的统计学的结论是：由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中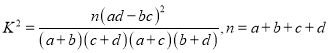
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
