
【题目】已知椭圆C:![]() (a>b>0)的焦点F与抛物线E:y2=4x的焦点重合,直线x-y+
(a>b>0)的焦点F与抛物线E:y2=4x的焦点重合,直线x-y+![]() =0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.
=0与以原点O为圆心,以椭圆的离心率e为半径的圆相切.
(Ⅰ)直线x=1与椭圆交于不同的两点M,N,椭圆C的左焦点F1,求△F1MN的内切圆的面积;
(Ⅱ)直线l与抛物线E交于不同两点A,B,直线l′与抛物线E交于不同两点C,D,直线l与直线l′交于点M,过焦点F分别作l与l′的平行线交抛物线E于P,Q,G,H四点.证明:![]()
【答案】(Ⅰ) ![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)利用条件得椭圆方程,将x=1代入椭圆得M,N坐标,求出△F1MN的周长和面积,进而得内切圆半径;
(Ⅱ)设出直线方程与椭圆联立,利用韦达定理结合弦长公式表示弦长,进而化简运算即可证明.
试题解析:
(Ⅰ) 依题意,得c=1,e=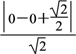 =
=![]() ,
,
即![]() =
=![]() ,∴a=2,∴b=
,∴a=2,∴b=![]() ,∴所求椭圆C的方程为
,∴所求椭圆C的方程为![]() +
+![]() =1.
=1.
直线l的方程为x=1,得M![]() ,N
,N![]() ,
,
设△F1MN的内切圆的半径为R,
则△F1MN的周长=4a=8,S△F1MN=![]() (|MN|+|F1M|+|F1N|)R=4R.
(|MN|+|F1M|+|F1N|)R=4R.
又因为S△F1MN=3=4R,∴R=![]() ,所求内切圆的面积为
,所求内切圆的面积为![]() π.
π.
(Ⅱ)设直线l和l′的方程分别为x=k1y+m1,x=k2y+m2,
设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由方程组![]() 得
得
y2-4k1y-4m1=0 ①
方程①的判别式Δ>0,得4k12+4m1>0.
由①得y1+y2=4k1,y1y2=-4m1,
由方程组![]() 得
得
y2-4k2y-4m2=0 ②
方程②的判别式Δ>0,得4k22+4m2>0.
由②得y3+y4=4k2,y3y4=-4m2.
联立直线l与直线l′的方程可得:M点坐标为![]() .
.
因为|MA|·|MB|=(1+k12)![]() ,代入计算得,
,代入计算得,
|MA|·|MB|=![]() ·|(m2-m1)2+4k1k2(m1+m2)-4(m1k22+m2k12)|.
·|(m2-m1)2+4k1k2(m1+m2)-4(m1k22+m2k12)|.
同理可得
|MC|·|MD|=(1+k22)![]() =
=
![]() ·
·![]() .
.
因此![]() =
=![]() .
.
由于PQ,HG分别与直线l和直线l′平行,故可设其方程分别为x=k1y+1,x=k2y+1.
由方程组![]() 得
得
y2-4k1y-4=0. ③
由③得yP+yQ=4k1,yPyQ=-4,
因此|PQ|=xP+xQ+p=k1(yP+yQ)+4=4(1+k12).
同理可得|HG|=xH+xG+p=k1(yH+yG)+4=4(1+k22).
故![]() =
=![]() .
.
所以![]() =
=![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数y=f(x),若同时满足下列条件:
①f(x)在D内单调递增或单调递减;
②存在区间[a,b]D,使f(x)在[a,b]上的值域为[a,b],则把y=f(x),x∈D叫闭函数.
(1)求闭函数y=x3符合条件②的区间[a,b];
(2)判断函数f(x)= ![]() x+
x+ ![]() ,(x>0)是否为闭函数?并说明理由;
,(x>0)是否为闭函数?并说明理由;
(3)已知[a,b]是正整数,且定义在(1,m)的函数y=k﹣ ![]() 是闭函数,求正整数m的最小值,及此时实数k的取值范围.
是闭函数,求正整数m的最小值,及此时实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 焦点
焦点![]() 且倾斜角的
且倾斜角的![]() 直线
直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]()
![]() 的面积为
的面积为![]() .
.
(I)求抛物线![]() 的方程;
的方程;
(II)设![]() 是直线
是直线![]() 上的一个动点,过
上的一个动点,过![]() 作抛物线
作抛物线![]() 的切线,切点分别为
的切线,切点分别为![]() 直线
直线![]() 与直线
与直线![]() 轴的交点分别为
轴的交点分别为![]() 点
点![]() 是以
是以![]() 为圆心
为圆心![]() 为半径的圆上任意两点,求
为半径的圆上任意两点,求![]() 最大时点
最大时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 ![]() 上的点按坐标变换
上的点按坐标变换  得到曲线
得到曲线 ![]() .
.
(1)求曲线 ![]() 的普通方程;
的普通方程;
(2)若点 ![]() 在曲线
在曲线 ![]() 上,点
上,点 ![]()
![]() ,当点
,当点 ![]() 在曲线
在曲线 ![]() 上运动时,求
上运动时,求 ![]() 中点
中点 ![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分,某考试每道都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道能排除两个错误选项,另2题只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机挑选一个选项做答,且各题做答互不影响.
(Ⅰ)求该考生本次测验选择题得50分的概率;
(Ⅱ)求该考生本次测验选择题所得分数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合U={x∈N|0<x≤8},S={1,2,4,5},T={3,5,7},则S∩(UT)=( )
A.{1,2,4}
B.{1,2,3,4,5,7}
C.{1,2}
D.{1,2,4,5,6,8}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数 ![]() 的图象和直线y=x无交点,现有下列结论:
的图象和直线y=x无交点,现有下列结论:
①方程f[f(x)]=x一定没有实数根;
②若a>0,则不等式f[f(x)]>x对一切实数x都成立;
③若a<0,则必存存在实数x0 , 使f[f(x0)]>x0;
④若a+b+c=0,则不等式f[f(x)]<x对一切实数都成立;
⑤函数 ![]() 的图象与直线y=﹣x也一定没有交点.
的图象与直线y=﹣x也一定没有交点.
其中正确的结论是(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
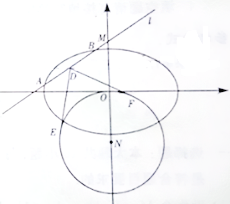
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,椭圆C截直线y=1所得线段的长度为
,椭圆C截直线y=1所得线段的长度为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)动直线l:y=kx+m(m≠0)交椭圆C于A,B两点,交y轴于点M.点N是M关于O的对称点,⊙N的半径为|NO|. 设D为AB的中点,DE,DF与⊙N分别相切于点E,F,求![]() EDF的最小值.
EDF的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com