【题目】已知椭圆
的左、右焦点分别为
，过点
的直线与椭圆
交于
两点，
的周长为8，直线
被椭圆截得的线段长为
.
（1）求椭圆的方程；
（2）设
是椭圆上两动点，线段
的中点为
，
的斜率分别为
（
为坐标原点），且
，求
的取值范围.
科目：高中数学 来源： 题型：
【题目】一袋中装有形状、大小都相同的6只小球，其中有3只红球、2只黄球和1只蓝球.若从中1次随机摸出2只球，则1只红球和1只黄球的概率为__________，2只球颜色相同的概率为________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.
若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列
，的前n项和为
，则下列说法中正确的是（ ）
A.数列是递增数列B.数列
是递增数列
C.数列的最大项是
D.数列的最大项是
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】Fibonacci数列又称黄金分割数列，因为当n趋向于无穷大时，其相邻两项中的前项与后项的比值越来越接近黄金分割数
．已知Fibonacci数列的递推关系式为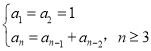
．
（1）证明：Fibonacci数列中任意相邻三项不可能成等比数列；
（2）Fibonacci数列{an}的偶数项依次构成一个新数列，记为{bn}，证明：{bn＋1-H2·bn}为等比数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的左、右焦点分别为
，
，椭圆的长轴长与焦距之比为
，过
且斜率不为
的直线
与交于
，
两点.
（1）当的斜率为
时，求
的面积；
（2）若在
轴上存在一点
，使
是以
为顶点的等腰三角形，求直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了得到函数
的图象，只需把函数
，
的图象上所有的点（ ）
A.向左平移
个单位长度，再把所得各点的横坐标伸长到原来的
倍（纵坐标不变）
B.向右平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）
C.向左平移个单位长度，再把所得各点的横坐标伸长到原来的
倍（纵坐标不变）
D.向右平移个单位长度，再把所得各点的横坐标伸长到原来的倍（纵坐标不变）
查看答案和解析>>
科目：高中数学 来源： 题型：
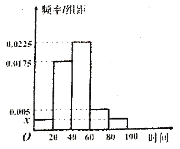
【题目】某高中随机抽取部分高一学生调查其上学路上所需时间(单位：分钟)，并将所得数据绘制成频率分布直方图（如图），其中上学路上所需时间的范围是
，样本数据分组为
，
，
，，
，
（Ⅰ）求直方图中
的值；
（Ⅱ）如果上学路上所需时间不少于1小时的学生可申请在学校住宿，若招生1200名，请估计新生中有多少名学生可以申请住宿；
（Ⅲ）从学校的高一学生中任选4名学生，这4名学生中上学路上所需时间少于40分钟的人数记为
，求的分布列和数学期望.（以直方图中频率作为概率）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
