
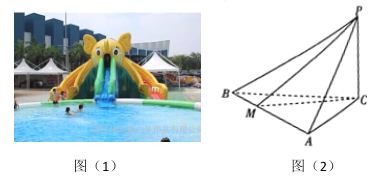
����Ŀ����ͼ��1����ijˮ�������ˮ������Ŀ��Ч��ͼ�����ǵ��ռ�Ͱ�ȫ�����ԭ������Ʒ������£���ͼ��2������ֱ����ˮ��Ŀ���ƽ̨![]() ���϶˵�P���ֱ���ˮ���ڵ�������ͬ����ˮ����
���϶˵�P���ֱ���ˮ���ڵ�������ͬ����ˮ����![]() ��
��![]() ��
��![]() ��ˮ�������¶˵�
��ˮ�������¶˵�![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ��
��![]() ƽ��
ƽ��![]() ������ˮ���ݵĻ������Կ����߶Σ�
������ˮ���ݵĻ������Կ����߶Σ�![]() ���ڹ�C����
���ڹ�C����![]() ��ֱ��ƽ���ڣ�Ϊ�˻��ݵİ�ȫ�ԣ����Ҫ��
��ֱ��ƽ���ڣ�Ϊ�˻��ݵİ�ȫ�ԣ����Ҫ��![]() .
.
��1�����ݵĸ�![]() �����ֵ��
�����ֵ��
��2�����ڿ����̿��ǰѸ�ˮ������Ŀ��Ƴ�����������Ŀ����Ϊ��֤����Ŀ��Ȥζ�ԣ����![]() ����û���װ�ã���ͼ��2���еļ����壩�������Сֵ.
����û���װ�ã���ͼ��2���еļ����壩�������Сֵ.
���𰸡���1��![]() m��2��562.5
m��2��562.5![]() .
.
��������
��1���ֱ����CB��CA��PC�ij����ֱ��ʾ�����![]() �������ò��ȹ�ϵ��⼴�ɣ�
�������ò��ȹ�ϵ��⼴�ɣ�
��2��������֪�������������ǹ���x�ĺ����������õ������б��������Сֵ����.
��1����![]() .
.
������֪![]() ��
��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ��
��
����![]() .
.
��Ϊ![]() ������
������![]() ��
��
����![]() .
.
���Ի����ĸ�![]() �����ֵΪ
�����ֵΪ![]() m.
m.
��2����Ϊ����![]() ���¶�Ϊ
���¶�Ϊ![]() ������
������![]() .
.
�ɣ�1��֪![]() ����
����![]() .
.
��![]() ������
������![]() .
.
��������P-ABC�����
![]() ��
��
���� ��
��
��![]() ʱ��
ʱ��![]() �����ݼ���
�����ݼ���
��![]() ʱ��
ʱ��![]() ����������
����������
���Ե�![]() ʱ��
ʱ��![]() ��
��
���Ըû���װ�õ������СΪ562.5m.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ��
��
��1����![]() ����
����![]() ��
��![]() �������߷��̣�
�������߷��̣�
��2�����������������![]() ��
��![]() ���������ʵ��
���������ʵ��![]() ��ֵ��
��ֵ��
��3��������![]() ����������ֵ�㣬��ʵ��
����������ֵ�㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�
�У�
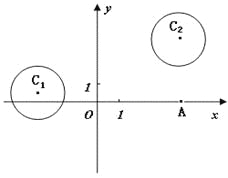
��֪Բ![]() ��Բ
��Բ![]() .
.
��1����ֱ��![]() ����
����![]() ���ұ�Բ
���ұ�Բ![]() �صõ��ҳ�Ϊ
�صõ��ҳ�Ϊ![]() ��
��
��ֱ��![]() �ķ��̣���2����PΪƽ���ϵĵ㣬���㣺
�ķ��̣���2����PΪƽ���ϵĵ㣬���㣺
���ڹ���P�������Ի��ഹֱ��ֱ��![]() ��
��![]() ��
��
���Ƿֱ���Բ![]() ��Բ
��Բ![]() �ཻ����ֱ��
�ཻ����ֱ��![]() ��Բ
��Բ![]()
�صõ��ҳ���ֱ��![]() ��Բ
��Բ![]() �صõ��ҳ���ȣ������������������ĵ�P�����ꡣ
�صõ��ҳ���ȣ������������������ĵ�P�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ����Բ
����Բ![]() �ij��᳤Ϊ4��
�ij��᳤Ϊ4��
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����ֱ֪��![]() ����Բ
����Բ![]() ����
����![]() ���㣬�Ƿ����ʵ��
���㣬�Ƿ����ʵ��![]() ʹ�����߶�
ʹ�����߶�![]() Ϊֱ����Բǡ�þ�������ԭ��
Ϊֱ����Բǡ�þ�������ԭ��![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�ļ���![]() ����
����![]() ����
����![]() ��
��![]() .ƽ��
.ƽ��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() .
.
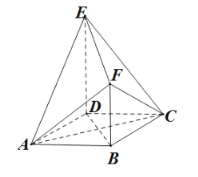
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л����崫ͳ�Ļ���ij��ѧѧ����Ա�У��һ�꼶1000��ѧ������ʱ��μӴ�ͳ�Ļ��������������ȡ50��ѧ�����е��飬�����ݷ����������б����£�
�μӳ��� | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�μ�����ռ���������İٷֱ� | 8% | 10% | 20% | 26% | 18% | 12% | 4% | 2% |
���Ƹ�У��һѧ���μӴ�ͳ�Ļ�������ȷ���ǣ�����
A. �μӻ������3����ѧ��ԼΪ360��B. �μӻ������2����4����ѧ��ԼΪ480��
C. �μӻ����������2����ѧ��ԼΪ280��D. �μӻ����������4����ѧ��ԼΪ360��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�������ķ����Ƿ��볣��̼�������йأ��ֶ�30����������е��飬�õ�������������
���� | ������ | ���� | |
���� | 2 | ||
������ | 18 | ||
���� | 30 |
��֪����30���������������ȡ1�����鵽����������ĸ���Ϊ![]() ��
��
��1���뽫������������������2���Ƿ���99.5%�İ�����Ϊ������ķ����볣��̼�������йأ�
�����Լ����ٽ�ֵ����
P��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�ο���ʽ��![]() ������n=a+b+c+d��
������n=a+b+c+d��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD��ֱ�����Σ�AB��CD��BC��CD������PABΪ�ȱ������Σ�AB��BC��2CD��2��
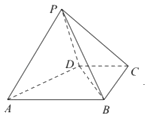
����֤����AB��PD��
������PD��2����ֱ��PC��ƽ��PAB���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
(1)�жϺ���![]() ��
��![]() �ϵĵ�����
�ϵĵ�����
(2)��![]() �������������
�������������![]() �����ֵ
�����ֵ
(3)��֤��![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com