
设a>0,a≠1,解关于x的不等式![]()
当0<a<1时,原不等式的解集为
{x|-![]() <x<-
<x<-![]() }∪{x|
}∪{x|![]() <x<
<x<![]() };
};
当a>1时,原不等式的解集为 {x|-∞<x<+∞}..
本小题考查指数函数性质、解不等式及综合分析能力.满分12分.
解法一 原不等式可写成 ![]() . ① ——1分
. ① ——1分
根据指数函数性质,分为两种情形讨论:
(Ⅰ)当0<a<1时,由①式得
x4-2x2+a2<0, ② ——3分
由于0<a<1时,判别式
△=4-4a2>0,
所以②式等价于
|
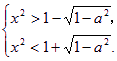 ——5分
——5分 解③式得 x<-![]() 或x>
或x>![]() ,
,
解④式得 -![]() <x<
<x<![]() . ——7分
. ——7分
所以,0<a<1时,原不等式的解集为
{x|-![]() <x<-
<x<-![]() }∪{x|
}∪{x|![]() <x<
<x<![]() }.
}.
——8分
(Ⅱ) 当a>1时,由①式得
x4-2x2+a2>0, ⑤ ——9分
由于a>1,判别式△<0,故⑤式对任意实数x成立,即得原不等式的解集为
{x|-∞<x<+∞}. ——12分
综合得
当0<a<1时,原不等式的解集为
{x|-![]() <x<-
<x<-![]() }∪{x|
}∪{x|![]() <x<
<x<![]() };
};
当a>1时,原不等式的解集为
{x|-∞<x<+∞}.
解法二 原不等式可写成 ![]() . ① ——1分
. ① ——1分
(Ⅰ) 当0<a<1时,由①式得
x4-2x2+a2<0, ② ——3分
分解因式得 (x2-1+![]() )(x2-1-
)(x2-1-![]() )<0. ③
)<0. ③
|
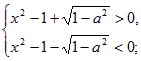
|
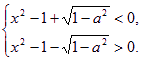 ——5分
——5分 解由④、⑤组成的不等式组得
-![]() <x<-
<x<-![]() .
.
或 ![]() <x<
<x<![]() . ——7分
. ——7分
由⑥、⑦组成的不等式组解集为空集;所以,0<a<1时,原不等式的解集为
{x|-![]() <x<-
<x<-![]() }∪{x|
}∪{x|![]() <x<
<x<![]() };
};
——8分
(Ⅱ) 当a>1时,由①式得
x4-2x2+a2>0, ⑧ ——9分
配方得 (x2-1)2+a2-1>0, ⑨
对任意实数x,不等式⑨都成立,即a>1时,原不等式的解集为
{x|-∞<x<+∞}. ——12分
综合得
当0<a<1时,原不等式的解集为
{x|-![]() <x<-
<x<-![]() }∪{x|
}∪{x|![]() <x<
<x<![]() };
};
当a>1时,原不等式的解集为 {x|-∞<x<+∞}.


科目:高中数学 来源:2014届宁夏高二上学期期末考试文科数学试卷(解析版) 题型:选择题
分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0”,求证 “ ”索的因应是( )
”索的因应是( )
A.a-b>0 B.a-c>0
C.(a-b)(a-c)>0 D.(a-b)(a-c)<0.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三上学期第三次理科数学测试卷(解析版) 题型:解答题
设a>0且a≠1,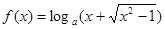 (x≥1)
(x≥1)
(Ⅰ)求函数f(x)的反函数f-1(x)及其定义域;
(Ⅱ)若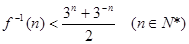 ,求a的取值范围。
,求a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com