
【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.
(Ⅰ)求y关于r的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的r.
科目:高中数学 来源: 题型:
【题目】如图所示,一块形状为四棱柱的木料, ![]() 分别为
分别为![]() 的中点.
的中点.
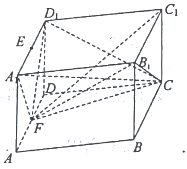
(1)要经过![]() 和
和![]() 将木料锯开,在木料上底面
将木料锯开,在木料上底面![]() 内应怎样画线?请说明理由;
内应怎样画线?请说明理由;
(2)若底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,
, ![]() 平面
平面![]() ,且
,且![]() ,求几何体
,求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对任意实数
对任意实数![]() 均有
均有![]() ,其中常数
,其中常数![]() 为负数,且
为负数,且![]() 在区间
在区间![]() 上有表达式
上有表达式![]() .
.
(1)写出![]() 在
在![]() 上的表达式,并写出函数
上的表达式,并写出函数![]() 在
在![]() 上的单调区间(不用过程,直接写出即可);
上的单调区间(不用过程,直接写出即可);
(2)求出![]() 在
在![]() 上的最小值与最大值,并求出相应的自变量的取值.
上的最小值与最大值,并求出相应的自变量的取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的函数
的函数![]() 为
为![]() 上的偶函数,且在区间
上的偶函数,且在区间![]() 上的最大值为10. 设
上的最大值为10. 设![]() .
.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 是否存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有四个不相等的实 数根?如果存在,求出实数
有四个不相等的实 数根?如果存在,求出实数![]() 的范围,如果不存在,说明理由.
的范围,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
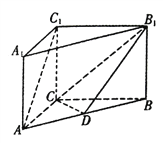
【题目】直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的动点.
上的动点.
(1)当点![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,试求出
?若存在,试求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acos A,则sin A:sin B:sin C为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com