
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当a=1时,求函数![]() 的单调区间:
的单调区间:
(Ⅱ)求函数![]() 的极值;
的极值;
(Ⅲ)若函数![]() 有两个不同的零点,求a的取值范围。
有两个不同的零点,求a的取值范围。
【答案】(Ⅰ)单调减区间为(1,+![]() ) ,增区间为(0,1); (Ⅱ)见解析(Ⅲ)a>1
) ,增区间为(0,1); (Ⅱ)见解析(Ⅲ)a>1
【解析】
(Ⅰ)当a=1, f′(x)=![]() ,解f′(x)<0和f′(x)>0确定单调区间;(Ⅱ)f′(x)
,解f′(x)<0和f′(x)>0确定单调区间;(Ⅱ)f′(x)![]() ,讨论a≤0和a>0时f′(x)的符号,确定单调性和极值;(Ⅲ)由(Ⅱ)知当 a≤0时,f(x)至多有一个零点,舍去;当a>0时,函数的极小值为f(a)=
,讨论a≤0和a>0时f′(x)的符号,确定单调性和极值;(Ⅲ)由(Ⅱ)知当 a≤0时,f(x)至多有一个零点,舍去;当a>0时,函数的极小值为f(a)=![]() 设函数g(x)=lnx+x-1,求导确定g(x):当0<x<1时,g(x)<0;x>1时,g(x)>0,分情况讨论:当0<a≤1,f(a)=ag(a) ≤0,f(x)至多有一个零点,不符合题意;当a>1时,由零点存在定理确定(
设函数g(x)=lnx+x-1,求导确定g(x):当0<x<1时,g(x)<0;x>1时,g(x)>0,分情况讨论:当0<a≤1,f(a)=ag(a) ≤0,f(x)至多有一个零点,不符合题意;当a>1时,由零点存在定理确定(![]() )和(a,3a-1)各有一个零点,则a可求
)和(a,3a-1)各有一个零点,则a可求
(Ⅰ)当a=1时,![]() , f′(x)=
, f′(x)=![]()
当f′(x)<0时,x>1; f′(x)>0时,0<x<1
∴函数![]() 的单调减区间为(1,+
的单调减区间为(1,+![]() ) ,增区间为(0,1)
) ,增区间为(0,1)
(Ⅱ)f(x)的定义域是(0,+∞),
f′(x)![]() ,
,
若a≤0,则f′(x)<0,此时f(x)在(0,+∞)递减,无极值
若a>0,则由f′(x)=0,解得:x=a,
当0<x<a时,f′(x)>0,当x>a时,f′(x)<0,
此时f(x)在(0,a)递增,在(a,+∞)递减;
∴当x=a时,函数的极大值为f(a)=![]() ,无极小值
,无极小值
(Ⅲ)由(Ⅱ)可知
当 a≤0时,f(x)在(0,+∞)递减,则f(x)至多有一个零点,不符合题意,舍去;
当a>0时,函数的极小值为f(a)=![]() ,
,
令g(x)=lnx+x-1(x>0)
∵![]() ∴g(x)在(0,+∞)单调递增,又g(1)=0, ∴0<x<1时,g(x)<0;x>1时,g(x)>0
∴g(x)在(0,+∞)单调递增,又g(1)=0, ∴0<x<1时,g(x)<0;x>1时,g(x)>0
(i) 当0<a≤1,f(a)=ag(a) ≤0,则函数f(x)至多有一个零点,不符合题意,舍去;
(ii) 当a>1时,f(a)=ag(a)>0
∵![]() ∴函数f(x)在(
∴函数f(x)在(![]() )内有一个零点,
)内有一个零点,
∵f(3a-1)=aln(3a-1)-![]()
设h(x)=lnx-x(x>2)
∵![]() ∴h(x)在(2,+∞)内单调递减,则h(3a-1)<h(2)=ln2-2<0
∴h(x)在(2,+∞)内单调递减,则h(3a-1)<h(2)=ln2-2<0
∴函数f(x)在(a,3a-1)内有一个零点.则当a>1时,函数f(x)恰有两个零点
综上,函数![]() 有两个不同的零点时,a>1
有两个不同的零点时,a>1


科目:高中数学 来源: 题型:
【题目】某研究机构对某校高二文科学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)试根据(2)中求出的线性回归方程,预测记忆力为14的学生的判断力.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且
且![]() .
.
(Ⅰ) 若1是关于x的方程![]() 的一个解,求t的值;
的一个解,求t的值;
(Ⅱ) 当![]() 且
且![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅲ)若函数![]() 在区间(-1,2]上有零点,求t的取值范围.
在区间(-1,2]上有零点,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一段长度为![]() 的木棍,希望将其锯成尽可能多的小段,要求每一小段的长度都是整数,并且任何一个时刻,当前最长的一段都严格小于当前最短的一段长度的2倍,记对
的木棍,希望将其锯成尽可能多的小段,要求每一小段的长度都是整数,并且任何一个时刻,当前最长的一段都严格小于当前最短的一段长度的2倍,记对![]() 符合条件时的最多小段数为
符合条件时的最多小段数为![]() ,则( )。
,则( )。
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,平面PCD⊥平面ABCD,![]() ,∠BAD=∠CDA=90°,
,∠BAD=∠CDA=90°,![]() .
.

(1)求证:平面PAD⊥平面PBC;
(2)求直线PB与平面PAD所成的角;
(3)在棱PC上是否存在一点E使得直线![]() 平面PAD,若存在求PE的长,并证明你的结论.
平面PAD,若存在求PE的长,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
(附:线性回归方程![]() 中,
中,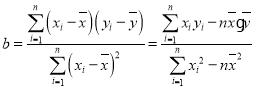 ,其中
,其中![]() ,
,![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=log2(kx2+4kx+3).①若f(x)的定义域为R,则k的取值范围是_____;②若f(x)的值域为R,则k的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com