
【题目】已知函数f(x)![]() 若方程2[f(x)]2﹣5tf(x)+3t2=0恰有4个不同的实根,则实数t的取值范围为(参考数据:ln2≈0.6931)( )
若方程2[f(x)]2﹣5tf(x)+3t2=0恰有4个不同的实根,则实数t的取值范围为(参考数据:ln2≈0.6931)( )
A.(![]() ,
,![]() )
)
B.(![]() ,
,![]() )
)
C.(![]() ,2﹣2ln2)∪(
,2﹣2ln2)∪(![]() ,1)
,1)
D.(![]() ,2﹣1n2)
,2﹣1n2)
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求出圆![]() 的直角坐标方程;
的直角坐标方程;
(2)已知圆![]() 与
与![]() 轴相交于
轴相交于![]() ,
, ![]() 两点,直线
两点,直线![]() :
: ![]() 关于点
关于点![]() 对称的直线为
对称的直线为![]() .若直线
.若直线![]() 上存在点
上存在点![]() 使得
使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 、
、![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 、
、![]() 之间的一-组相关数据如下表所示,则下列说法错误的是( )
之间的一-组相关数据如下表所示,则下列说法错误的是( )
|
|
|
|
|
|
|
|
|
|
A.可以预测,当![]() 时,
时,![]() B.
B.![]()
C.变量![]() 、
、![]() 之间呈负相关关系D.该回归直线必过点
之间呈负相关关系D.该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个命题:
,给出下列四个命题:
①![]() 的最小正周期为
的最小正周期为![]()
②![]() 的图象关于直线
的图象关于直线![]() 对称
对称
③![]() 在区间
在区间![]() 上单调递增
上单调递增
④![]() 的值域为
的值域为![]()
⑤![]() 在区间
在区间![]() 上有6个零点
上有6个零点
其中所有正确的编号是( )
A.②④B.①④⑤C.③④D.②③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
(1)求实数k的值,并讨论函数f(x)的单调性;
(2)设函数g(x)![]() ,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代在珠算发明之前多是用算筹为工具来记数、列式和计算的.算筹实际上是一根根相同长度的小木棍,如图,算筹表示数1~9的方法有“纵式”和“横式”两种,规定个位数用纵式,十位数用横式,百位数用纵式,千位数用横式,万位数用纵式,…,以此类推,交替使用纵横两式.例如:627可以表示为“![]() ”.如果用算筹表示一个不含“0”且没有重复数字的三位数,这个数至少要用7根小木棍的概率为( )
”.如果用算筹表示一个不含“0”且没有重复数字的三位数,这个数至少要用7根小木棍的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1 km处,tan∠BAN=![]() ,∠BCN=
,∠BCN=![]() ,.现计划铺设一条电缆连通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元km、4万元km.
,.现计划铺设一条电缆连通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元km、4万元km.
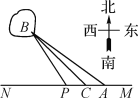
(1)求A,B两镇间的距离;
(2)应该如何铺设,使总铺设费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究不同性别在处理多任务时的表现差异,召集了男女志愿者各200名,要求他们同时完成多个任务,包括解题、读地图、接电话.下图表示了志愿者完成任务所需的时间分布.以下结论,对志愿者完成任务所需的时间分布图表理解正确的是( )

①总体看女性处理多任务平均用时更短;
②所有女性处理多任务的能力都要优于男性;
③男性的时间分布更接近正态分布;
④女性处理多任务的用时为正数,男性处理多任务的用时为负数.
A.①④B.②③C.①③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com